 Die chemische Bindung im Anfängerunterricht – ein offenes Modell
Die chemische Bindung im Anfängerunterricht – ein offenes Modell  Die chemische Bindung im Anfängerunterricht – ein offenes Modell
Die chemische Bindung im Anfängerunterricht – ein offenes Modell Wenn Sie diesen Text oder Teile davon ausdrucken möchten, verwenden Sie am Besten die pdf-Version. Anregungen und Kommentare bitte an kluef@cup.uni-muenchen.de.
Die folgenden Begriffe beschreiben einen Weg vom Atombau zur kovalenten Bindung (Elektronenpaarbindung, Atombindung). Ziel ist ein offenes Modell, dass eine echte Teilmenge einer umfassenden Beschreibung darstellt. Eine solches „korrektes“ Modell (vulgo: die Wahrheit) lässt sich durch Ergänzungen immer weiter ausbauen, ohne dass Einzelaspekte zurückgenommen werden müssen. Im Mittelpunkt steht – im Einklang mit dem Stand der Computerchemie – die Oktettregel, die konsequent angewendet wird, und die Energie der beteiligten Atomorbitale. Stark beschnitten wird das VSEPR-Modell, das Oktettüberschreitung zulässt.
Die Bausteine im Einzelnen:
Nachdem aus den stöchiometrische Gesetzen ein Atombegriff abgeleitet wurde (Atome als massebehaftete kleinste Teilchen chemischer Elemente), zeigen Linienspektren die Notwendigkeit, die Energie von Elektronen durch Quantenzahlen darzustellen.
Das Bohrsche Atommodell zeigt das Prinzip: es gelingt durch 1 Quantenzahl, der Hauptquantenzahl, die Balmer-Serie in ein Schema elektronischer Energien zu übertragen (später: Orbitalenergien).
Mehrelektronen-Atome benötigen insgesamt 4 Quantenzahlen, wobei die Hauptquantenzahl, die Nebenquantenzahl und die Orientierungsquantenzahl durch eine hierarchische Ordnung miteinander verbunden sind.
Eine gegebene Kompbination dieser drei Quantenzahlen definiert ein Orbital, in das bis zu zwei Elektronen mit unterschiedlicher Spinquantenzahl eingefüllt werden können.
Unter Beachtung der energetischen Abfolge der Orbitale lässt sich durch das Aufbauprinzip das Periodensystem der Elemente ableiten.
Die Orbitale entsprechen dreidimensionalen stehenden Wellen, deren Eigenschaften sich aus niederdimensionalen Analoga erschließt: die Knotenebenen aus eindimensional stehenden Wellen (Violinsaite), und das Verhalten bei der Überlagerung („Orbitalüberlappung“) aus dem Verhalten zweidimensionaler fortschreitender Wellen (Wellenmuster auf Wasser).
Ein einfacher Fall wie die Valenzschale des Neons zeigt das Prinzip der Zunahme an Knotenebenen mit zunehmender Energie (abnehmender Stabilität).
Die Bedeutung der Valenzschale selbst ergibt sich aus den Orbitalenergien, die mit messbaren Größen wie den Ionisierungsenergien, der Elektronenaffinität und der Elektronegativität verbunden ist. Auch die Oktettregel ergibt sich an diesem Punkt.
Die kovalente Bindung wird durch die Überlagerung von Atomorbitalen eingeführt.
Lewis-Formeln, bei denen die Oktettregel eingehalten wird, sind ein adäquates Mittel, um ein Molekül zu beschreiben.
Molekülorbitale und lokalisierte Bindungen sind äquivalente Beschreibungen des Bindungszustands eines Moleküls.
Am Methanmolekül zeigt sich, dass die gleichwertige Beteiligung von s- und p-Orbitalen am Bindungszustand des Moleküls auch aus einer MO-Betrachtung hervorgeht; auch die sp3-Hybridisierung des C-Atoms lässt sich aus einer MO-Behandlung ableiten.
Fazit: während eine MO-Behandlung bei schulrelevanten Molekülen bestenfalls bei O2 und bei den Aromaten nötig ist, lassen sich bei Hauptgruppenelementatomen aus einer Betrachtung der s- und p-Orbitale der Valenzschale einschließlich ihrer charakteristischen Orbitalenergien zahlreiche Einzelheiten ableiten: der Aufbau des Periodensystems, die Oktettregel, Atomeigenschaften (Ionisierungsenergie, Elektronenaffinität, Elektronegativität), die Struktur zahlreicher Moleküle durch Spinpaarung zwischen einfach besetzten Atomorbitalen. Da die quantitative Behandlung bei Hauptgruppenelementen zu keiner nennenswerten d-Orbitalbeteiligung führt, gilt hier die Oktettregel streng. Eine Oktettüberschreitung bei Molekülen wie SO2 oder H2SO4 sollte zugunsten partiell ionischer Formulierungen vermieden werden. Das VSEPR-Modell mit seinem sorglosen Umgang der Oktettüberschreitung (bei zugleich vollständiger Hybridisierung) hat hier Schwächen: es sagt die Struktur eines ClF3 ganz gut voraus, legt aber die Existenz eines ClH3 = H3Cl nahe. Während das Rezept „paare zur Bildung von Molekülen die Elektronen der Atome in deren Grundzustand“ zum Beispiel beim S8-Molekül dessen p-p-Bindungen sehr gut beschreibt und das s-Orbital einem freien Elektronenpaar zuweist, sind die wichtigen Moleküle NH3, H2O und viele organischen Moleküle durch die vollständige Einbeziehung des s-Orbitals in die Bindung charakterisiert; spn-Hybride sind adäquat, um dies zu beschreiben.
Die folgenden Seiten sind Auszüge aus der Chemischen Grundvorlesung an der LMU München im Wintersemester 2008/2009. Die vollständige Vorlesung liegt als Internet-Skript vor.
Atome sind aus den Nucleonen (Protonen, Neutronen) und Elektronen aufgebaut. Während das Auftreten von Isotopen aus dem Aufbau des Atomkerns verständlich wird, resultieren die chemischen Eigenschaften aus der Elektronenstruktur. Im Mittelpunkt der Betrachtung steht die Beschreibung elektronischer Zustände durch die vier Quantenzahlen n, l, ml und ms. Von diesen wird zuerst die Hauptquantenzahl n eingeführt, mit deren Hilfe sich die Lage der Emissionslinien im Wasserstoffspektrum deuten lassen. Anschließend werden die elektronischen Aufenthaltsräume, die Orbitale, im Detail betrachtet. Die Zuordnung von Elektronenkonfigurationen zu den Grundzuständen der Atome führt zum Periodensystem der Elemente (PSE). Umgekehrt zeigen Atomeigenschaften wie die Ionisierungsenergie oder die Elektronenaffinität einen charakteristischen Gang im PSE.
| Mortimer: 2, 6 Binnewies: 2, 3 Riedel: 1.2, 1.4 |
Die kleinsten Teilchen eines chemischen Elementes, die Atome, sind aus den Elementarteilchen Elektronen, Protonen und Neutronen aufgebaut, die sich in Masse und elektrischer Ladung unterscheiden. Der Atomkern wird durch positiv geladene Protonen der relativen Masse 1,007277 und der Ladung +e sowie durch elektrisch neutrale Neutronen der Masse 1,008665 gebildet. Elektronen sind gegenüber den Kernteilchen, den Nukleonen, nahezu masselos (ca. 1/2000), sie tragen die Ladung −e. 1 e ist die Elementarladung, die kleinste elektrische Ladung; alle auftretenden Ladungsmengen sind ganzzahlige Vielfache dieser Elementarladung. Ihr Betrag ist:
1 e = 1,6022 × 10−19 C
Die Radien der Atomkerne sind von der Größenordnung 10−2 bis 10−3 pm (1 pm = 10−12 m; vergleiche zum Beispiel den Radius eines Kupferatoms von 128 pm, vgl. das Rutherfordsche Experiment). Der im Vergleich zum gesamten Atom sehr kleine Atomkern enthält fast die gesamte Masse des Atoms. Die Zahl der Protonen bestimmt die Größe der positiven Ladung des Kerns, die Kernladungszahl, die der Protonenzahl gleich ist. Die Gesamtzahl der Protonen und Neutronen bestimmt die Masse des Kerns und angenähert die des Atoms, sie wird daher Massenzahl genannt. Ein chemisches Element besteht aus Atomen gleicher Protonenzahl (Kernladungszahl), die Zahl der Neutronen kann jedoch unterschiedlich sein. Die für das Element charakteristische Protonenzahl wird auch Ordnungszahl genannt.
Eine durch Kernladungszahl und Neutronenzahl charakterisierte Atomsorte bezeichnet man als Nuklid. Nuklide mit gleicher Protonenzahl, aber verschiedener Neutronenzahl heißen Isotope. Beispiele sind die Isotope von Wasserstoff (beachte die übliche Schreibweise, die Massenzahl links oben und die Kernladungszahl links unten am Elementsymbol zu notieren): 21H, (= D, Deuterium), 31H (= T, Tritium).
Da die Information über die Ordnungszahl bereits durch das Atomsymbol gegeben wird, werden Nuklide oft nur durch die Massenzahl beschrieben, zum Beispiel bei den verschiedenen Kohlenstoffisotopen:
12C, 13C,14C
oder bei den Isotopen von Stickstoff:
14N, 15N
Die meisten Elemente sind Mischelemente, die aus mehreren Isotopen in oft sehr unterschiedlicher Häufigkeit bestehen. So werden die Isotope von Wasserstoff, Kohlenstoff und Stickstoff mit folgenden Häufigkeiten gefunden: 1H (99,985 %), 2H (0,015 %); 12C (98,89 %), 13C (1,11 %); 14N (99,63 %), 15N (0,36 %).
Einige Elemente sind Reinelemente, die in ihrem natürlichen Vorkommen aus nur einer Nuklidsorte bestehen (zum Beispiel Fluor nur 19F, Natrium nur 23Na). Nuklide mit gleicher Massenzahl, aber unterschiedlicher Kernladungszahl werden Isobare genannt (zum Beispiel 14C, 14N).
Die Untersuchung von Emissionsspektren zeigt eine wesentliche Eigenschaft der Elektronen – die Quantelung der Energiezustände. Atome in einem angeregten elektronischen Zustand können durch Zufuhr thermischer oder elektrischer Energie erzeugt werden. Bei der Rückkehr in den elektronischen Grundzustand wird die Energiedifferenz zum angeregten Zustand oft in Form von Lichtenergie abgestrahlt. Die spektrale Zerlegung des erzeugten Strahlung ergibt Linienspektren als Indiz für diskrete Energiezustände, die von den Elektronen eingenommen werden können.
Versuch 6-1: Li-, Na-, B-Flammenfärbung
Versuch 6-2: Plücker-Röhre (Wasserstoff und Stickstoff) • An einem Glasrohr liegt Hochspannung an. Das Rohr wird mit Wasserstoff gefüllt und anschließend evakuiert. Mit dem Erreichen eines hinreichenden Vakuums beginnt die Röhre blauviolett zu leuchten. Die Leuchterscheinung ist die Mischfarbe der im folgenden Bild dargestellten Spektrallinien.
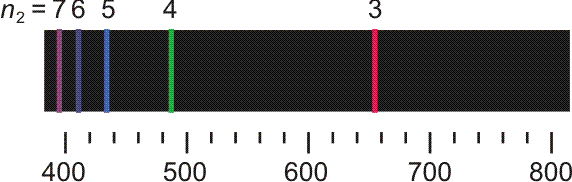
Die ersten fünf Linien der Balmer-Serie. Unter dem Emissionspektrum ist die Wellenlänge in nm angegeben, oberhalb des Spektrums n2, die Hauptquantenzahl des angeregten Zustands. Der energieärmere Zustand liegt bei der Balmer-Serie bei n1 = 2.
Noch bevor eine erklärende Modellvorstellung erkannt wurde, gelang es, eine einfache Beziehung aufzustellen, welche die Lage der Linien in der abgebildeten „Balmer-Serie“ beschreibt: Für n ≥ 3 gilt nämlich (Frequenz ν, Wellenlänge λ):
ν = c λ−1 = 3,289 × 1015 × (1/4 − 1/n2) sec−1
Die Suche nach weiteren Serien in den nicht sichtbaren Bereichen des elektromagnetischen Spektrums führte zu der allgemeinen Beziehung:
ν = 3,289 × 1015 × (1/n12 − 1/n22) sec−1
für n2 ≥ n1. Besonders aufschlussreich ist es, für die Serie mit n1 = 1 – die im UV-Bereich beobachtbare Lyman-Serie – über die beobachteten Linien für n2 = 2, 3, 4, … auf n2 = ∞ zu extrapolieren. Die erhaltene Energie beträgt umgerechnet 13,6 eV. Dieser Betrag entspricht der Ionisierungsenergie des Wasserstoffatoms, das ist die Energie, die für den Vorgang
H → H+ + e−
aufgebracht werden muss (dieser Energiebetrag heißt auch Rydberg-Konstante; Sie finden ihn in den Lehrbüchern auch in anderen Energieeinheiten tabelliert). Es gelang N. Bohr, diese Beobachtungen durch ein Schalenmodell des Wasserstoffatoms zu deuten. Die Elektronen können in diesem Modell nur diskrete Energiezustände einnehmen, deren energieärmster, stabilster Zustand 13,6 eV unter der Ionisationsgrenze liegt, die bei 0 eV gesetzt wird (siehe Abbildung, zusammen mit der Balmer-Serie auch als pdf).

Orbitalenergieschema des Wasserstoffatoms. Die Energie eines Zustands hängt nur von der Hauptquantenzahl n ab, der „Schale“ im Bohrschen Atommodell. Die Ionisationsgrenze liegt beim Ordinatenwert 0. Die blauen Pfeile kennzeichnen die Elektronensprünge, durch welche die Balmer-Serie hervorgerufen wird.
Die erlaubten Zustände treten in immer dichterer Folge auf, je näher die Ionisationsgrenze rückt. Die Energiewerte folgen dabei der Reihe
| E = | 13,6 eV | mit n = 1, 2, 3, … |
| n2 |
n ist eine „Quantenzahl“, mit der eine Elektronenenergie eindeutig beschrieben ist; im Bohrschen Modell wird n als die Nummer der „Schale“ interpretiert, auf der das Elektron um den Kern kreist. Man beachte, dass das Bohrsche Atommodell das Elektron als Teilchen behandelt. So wird die Rydberg-Konstante RH in diesem Modell abgeleitet als (reduzierte Masse μ, Ladung Z, Vakuum-Dielektrizitätskonstante ε0):
| RH = | μ Z2 e4 |
| 8 ε02 h2 |
Es tritt die reduzierte Masse μ auf; für das Wasserstoffnuklid 1H gilt: 1/μ = 1/mProton + 1/mElektron. Die Behandlung des Elektrons als rotierende Masse ist offensichtlich.
Dem Bohrschen Atommodell folgte die wellenmechanische Behandlung der Elektronenstruktur. Eine mathematische Ausarbeitung wird an dieser Stelle nicht gegeben. In Vorlesungen zur Quantenmechanik werden Sie ableiten, dass die „Schale“ des Bohrschen Atommodells nur eine von vier Quantenzahlen darstellt, die den Zustand eines Elektrons eindeutig festlegen. Die ersten drei Quantenzahlen folgen dabei einem hierarchischen Schema, an dessen Ausgangspunkt die Hauptquantenzahl n steht:
Die Hauptquantenzahl kann die Werte n = 1, 2, 3, … annehmen.
Mögliche Werte für die Nebenquantenzahl l sind l = 0, 1, 2, … (n − 1); für l gibt es also n mögliche Werte.
Mögliche Werte für die magnetische oder Orientierungsquantenzahl ml sind ml = −l, …, 0, …, +l; ml hängt damit von l ab, es gibt 2 l + 1 mögliche Werte.
Unabhängig von n, l und ml ist die (magnetische) Spinquantenzahl ms, welche die Werte +½ und −½ annehmen kann.
Man beachte, dass die Hauptquantenzahl n die möglichen Werte für die Nebenquantenzahl l festlegt und diese die möglichen Werte für die Orientierungsquantenzahl ml. Neben der Bezeichnung durch Zahlen werden Quantenzahlen auch durch Buchstaben beschrieben; es gelten die folgenden Symbole:
| n | l | |
|---|---|---|
| 0 | s | |
| 1 | K | p |
| 2 | L | d |
| 3 | M | f |
Unter einem „2p-Elektron“ ist danach ein Elektron der Hauptquantenzahl 2 und der Nebenquantenzahl 1 zu verstehen; „Elektronen der L-Schale“ sind Elektronen der Hauptquantenzahl 2. Bei der Besetzung der Energieniveaus gilt das Pauli-Verbot: Es stimmen niemals alle vier Quantenzahlen von Elektronen eines Atoms überein. Die Hauptquantenzahl 1 kann daher für höchstens zwei Elektronen zutreffen (n = 1; l = 0; ml = 0; ms = +½ oder −½) und die Hauptquantenzahl 2 für höchstens acht Elektronen (n = 2; l = 0, 1; ml = 0 für l = 0, ml = −1, 0, +1 für l = 1; ms = +½ oder −½). Allgemein können 2 n2 Elektronen dieselbe Hauptquantenzahl aufweisen („in der selben Schale sein“), während sich bei vorgegebener Haupt- und Nebenquantenzahl die folgenden maximalen Elektronenzahlen ergeben:
2 Elektronen im Zustand ns, 6 bei np, 10 bei nd und 14 bei nf.
Die Energien der einzelnen Niveaus hängen von n und l ab; ihre Abfolge ist:
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, …
Beachten Sie, dass hinter der in vielen Lehrbüchern gezeigten Eselsbrücke, die diese Reihenfolge aus einem Schachbrettmuster ableitet, kein Naturgesetz steht.
In einem Atom im Grundzustand besetzen die Elektronen die erlaubten Energieniveaus mit der niedrigsten Energie, wobei die Hundsche Regel beachtet wird: Zustände gleicher Energie werden zunächst mit jeweils einem Elektron besetzt.
Im Periodensystem der Elemente sind die Elemente in der Folge ihrer Elektronenzahlen (= Kernladungszahlen = Ordnungszahlen) angeordnet. Eine eindeutige Zuordnung ergibt sich durch das Moseleysche Gesetz, auf das weiter unten eingegangen wird.
Das gewohnte Langperiodensystem entsteht, wenn Blöcke entsprechend den Nebenquantenzahlen gebildet werden, wenn also alle s-Elemente untereinander, alle p-Elemente untereinander, usw., angeordnet werden; Elemente, deren Elektronen höchster Energie die gleiche Hauptquantenzahl aufweisen, werden dabei in eine Zeile (Periode) geschrieben:
| n | s-Block | d-Block | p-Block | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | … | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| 1 | 1H | 2He | |||||||||
| 2 | 3Li | 4Be | 5B | 6C | 7N | 8O | 9F | 10Ne | |||
| 3 | 11Na | 12Mg | 13Al | 14Si | 15P | 16S | 17Cl | 18Ar | |||
| 4 | 19K | 20Ca | 21Sc | … | 30Zn | 31Ga | 32Ge | 33As | 34Se | 35Br | 36Kr |
Auf diese Weise kommen Elemente mit gleicher Elektronenanordnung in der äußersten Schale untereinander zu stehen; diese gleiche Anordnung der Elektronen der unvollständig gefüllten Schale, der Valenzelelektronen bedingt ähnliche chemische Eigenschaften solcher Elemente einer Gruppe des Periodensystems (beachte eine Abweichung von der Regel: Helium, He, steht trotz seiner beiden Elektronen im 1s-Zustand nicht über Beryllium, Be, sondern in Übereinstimmung mit seinen chemischen Eigenschaften in der Gruppe der Edelgase).
Die Elemente des s-Blockes und des p-Blockes werden als Hauptgruppenelemente bezeichnet; bei diesen entspricht die Periodennummer der Hauptquantenzahl der Elektronen, die im Verlauf der Periode in ihr entsprechendes Niveau eingefüllt werden; die Gruppennummer entspricht nach alter Zählung der Zahl der Valenzelektronen, bei neuer Zählweise weist ein p-Block-Element der Gruppennummer i gerade i − 10 Valenzelektronen auf. Die Gruppennummer 18 entspricht einer vollständigen Auffüllung der s- und p-Niveaus einer Schale (Ausnahme: Für n = 1 ist die Schale mit zwei Elektronen gefüllt). Dies ist die Edelgaskonfiguration, die besonders stabile Elektronenanordnung der Edelgase.
Bei den Elementen des d-Blockes, den Nebengruppenelementen, werden Elektronen der Hauptquantenzahl n − 1 eingefüllt, obwohl schon Elektronen mit der Hauptquantenzahl n vorhanden sind. Die Elemente der ersten neun Nebengruppen, bei denen das d-Niveau nicht vollständig gefüllt ist, werden auch als Übergangselemente oder Übergangsmetalle bezeichnet. Bei den Elementen des f-Blockes schließlich werden Elektronen der Hauptquantenzahl n − 2 aufgefüllt.
Die 10 Elektronen des Edelgases Neon bilden die Elektronenkonfiguration 1s2 2s2 2p6. Die energetische Abfolge spiegelt die hohe Kernladungszahl des Neons im Vergleich zu Wasserstoff wider. Das Valenzelektronenkonzept wird deutlich, wenn die besondere Stabilität des 1s-Niveaus betrachtet wird (Abbildung auch als pdf):
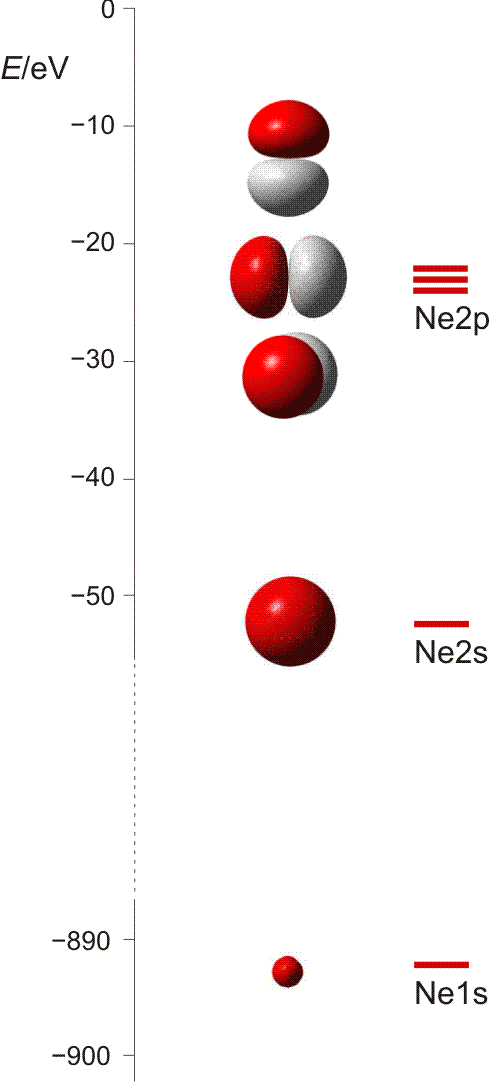
Die fünf besetzten Atomorbitale des Neons. Jedes Orbital ist mit einem spingekoppelten Elektronenpaar besetzt. Man beachte die starke Kontraktion und die hohe Stabilität des 1s-Orbitals.
In der Abbildung ist bei den einzelnen Orbitalen eine Gestalt angegeben. Im Teilchenmodell ist das Orbital mit dem Aufenthaltsraum des Elektrons verknüpft. Für die Deutung der chemischen Bindung im nächsten Kapitel ist es nützlicher, die durch n, l und ml charakterisierten Orbitale als dreidimensionale stehende Wellen anzusehen. Im Wellenmodell kommt zur Kontur des Orbitals eine Vorzeicheninformation hinzu, die bei einer zweidimensionalen Welle dem Wellenberg und -tal entspricht. In der Abbildung sind die verschiedenen Vorzeichen durch die Farben rot und grau unterschieden.
Versuch 6-3: Eindimensional stehende Wellen
Das 1s-Orbital ist kugelsymmetrisch, die zugehörige Wellenfunktion hat an jedem Ort des Raums ein positives Vorzeichen. Dasselbe scheint für das 2s-Orbital zu gelten, ein Schnitt durch das Orbital würde jedoch in Kernnähe einen Vorzeichenwechsel zeigen. Aufgrund der Kernnähe des Vorzeichenwechsels spielt dieser für die folgenden Bindungsbetrachtungen keine Rolle, da die Wechselwirkungen zwischen den Orbitalen zweier Atome durch die äußere Kontur dominiert wird.
Das 2p-Orbital zeigt einen Vorzeichenwechsel in der äußeren Kontur. Das Orbital besitzt eine durch den Kern verlaufende Knotenebene, in der die Wahrscheinlichkeit, das Elektron anzutreffen, Null ist. Man beachte, dass diese Aussage mit einer Teilchenvorstellung unverträglich ist. Die drei energiegleichen, „entarteten“ (engl. degenerate) p-Orbitale unterscheiden sich durch ihre Ausrichtung im Raum. Den drei Werten für ml entsprechen drei Orbitalausrichtungen entlang der drei Basisvektoren eines kartesischen Koordinatensystems. Zur Unterscheidung der drei p-Orbitale dienen alternativ zu ml = −1, 0 oder 1 die Bezeichnungen px, py und pz.
Man beachte eine im Folgenden wichtige Eigenschaft der gezeigten Neon-Orbitale: Werden zwei beliebige Orbitale einander überlagert, so ist der gemeinsame Raum, in dem gleiche Vorzeichen zusammentreffen und die Wellen einander verstärken (konstruktive Interferenz) genauso groß wie der Raum, in dem die Wellenfunktionen verschiedenes Vorzeichen haben und einander auslöschen (destruktive Interferenz) – die Nettoüberlappung ist 0, die Orbitale sind orthogonal.
Bei den folgenden Diskussionen der chemischen Eigenschaften von Atomen und Molekülen wird die Orbitalenergie im Bereich der Valenzelektronen eine wichtige Rolle spielen. Orbitalenergiediagramme verdeutlichen Trends im PSE, zum Beispiel bei der Ionisierungsenergie von Atomen oder deren Elektronenaffinität.
Die 1. Ionisierungsenergie („1. Ionisierungspotential“) I1 eines Atoms ist die Energie, die mindestens benötigt wird, um ein Elektron vollständig aus dem Atom zu entfernen. Aus dem Atom entsteht ein einfach positiv geladenes Ion:
X → X+ + e−
Die 1. Ionisierungsenergie entspricht weitgehend der Orbitalenergie des energiereichsten Elektrons. Die Entfernung des zweiten Elektrons erfordert die Energie I2, des dritten I3, und so fort. Ionisierungsenergien sind ein Maß für die Festigkeit, mit der Elektronen im Atom gebunden sind. I1 wächst innerhalb einer Periode von links nach rechts; das heißt, dass die Entfernung eines Elektrons umso schwerer fällt, desto kleiner ein Atom ist, desto näher also das betrachtete Elektron dem anziehenden Kern ist – siehe die vorige Abbildung. Für ein gegebenes Element wachsen die Ionisierungspotentiale in der Reihe I1, I2, I3, … schnell an, da die Entfernung von Elektronen aus einem zunehmend höher positiv aufgeladenen Atom immer mehr Energie erfordert. Die Entfernung eines Elektrons aus einer Edelgasschale bedingt einen auffälligen Sprung in der Folge der Ionisierungspotentiale (Abbildung auch als pdf).
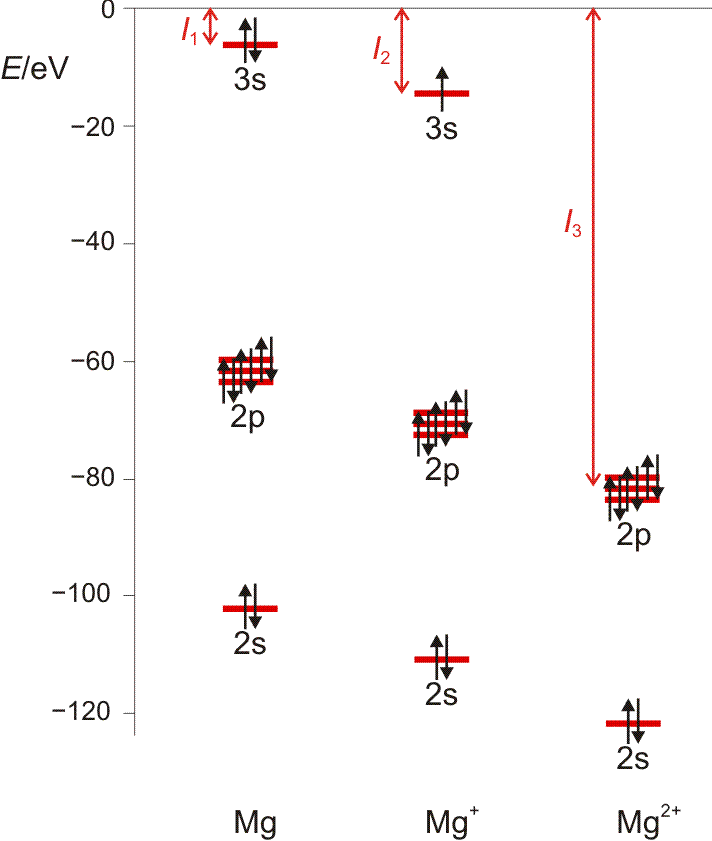
Orbitalenergien für Mg, Mg+ und Mg2+. Die Ionisierungsenergie wird benötigt, um das energiereichste Elektron zu entfernen. Man beachte den Sprung beim Wegfall der Valenzschale (technische Anmerkung: Orbitalenergien mit hf/6-31g(d,p), Mittelwerte für α- und β-Spin bei Mg+).
Die Elektronenaffinität (EA) eines Atoms ist die Energie, die frei wird oder benötigt wird, wenn ein Atom ein Elektron anlagert. Aus einem neutralen Atom wird dabei ein Anion:
X + e− → X−
Der enge Bezug zur Ionisierungsenergie wird klar, wenn der umgekehrte Vorgang betrachtet wird:
X− → X + e−
Die Elektronenaffinität erscheint nun vom Betrag her als Ionisierungsenergie des Anions; sie entspricht damit weitgehend der Orbitalenergie des höchsten besetzten Orbitals des Anions X−. Die folgende Abbildung (pdf) zeigt I1 und EA im Orbitalschema des Fluors:
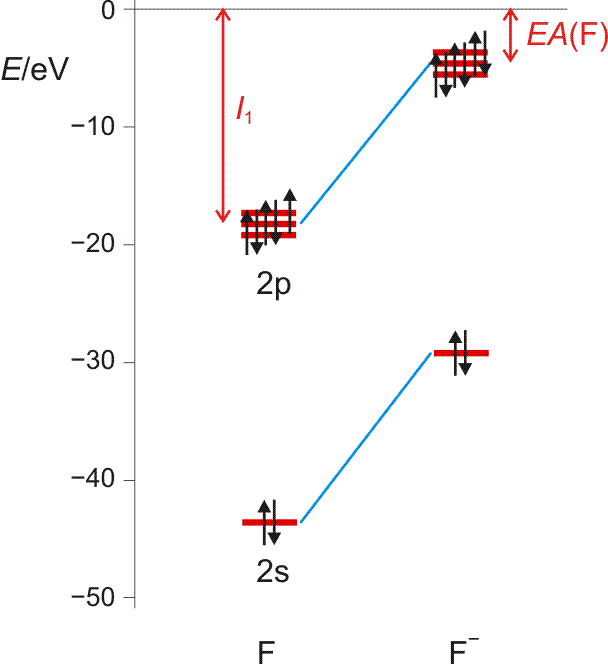
Die größten EA-Werte werden bei den Halogenen gefunden, die durch die Aufnahme eines Elektrons die Elektronenkonfiguration des im Periodensystems folgenden Edelgases erreichen. I1 und EA eines Atoms werden weiter unten noch einmal aufgegriffen, um bei der Behandlung der chemischen Bindung den wichtigen Begriff „Elektronegativität“ zu definieren.
Die konstruktive Interferenz einfach besetzter Atomorbitale führt zu bindenden Molekülorbitalen. Daneben sind nichtbindende und antibindende Kombinationen von Atomorbitalen zu beachten, wenn die Valenzelektronen zweier Atome in Wechselwirkung treten, um σ- und π-Bindungen aufzubauen. Die durch eine Lewis-Formel darstellbare kovalente 2e-2z-Bindung steht im Mittelpunkt der Valenzbindungsmethode („VB-Methode“), die aus der allgemeineren Molekülorbitalmethode („MO-Methode“) abgeleitet werden kann.
| Mortimer: 2, 6 Binnewies: 2, 3 Riedel: 1.2, 1.4 |
Wasserstoff kommt in Form von H2-Molekülen vor. Zwei H-Atome sind in diesen durch eine kovalente Bindung (Atombindung) miteinander verbunden. Die Ausbildung der Bindung lässt sich deuten, wenn wie bei der Besetzung von Atomorbitalen im vorigen Kapitel nach Molekülorbitalen gefragt wird, bei denen Elektronen nun aber mit mehr als einem Atomkern wechselwirken. Ein gedanklich naheliegendes Verfahren zur Konstruktion solcher Molekülorbitale (MOs) verbirgt sich hinter dem Kürzel LCAO (linear combination of atomic orbitals, Linearkombination von Atomorbitalen). Hierbei wird von Atomorbitalen ausgegangen und deren Wechselwirkung miteinander untersucht. Das Bild der stehenden Welle hilft dabei, eine Verstärkung oder eine Schwächung der Welle zu identifizieren (konstruktive oder destruktive Interferenz). Das Prinzip geht aus der folgenden Abbildung hervor.
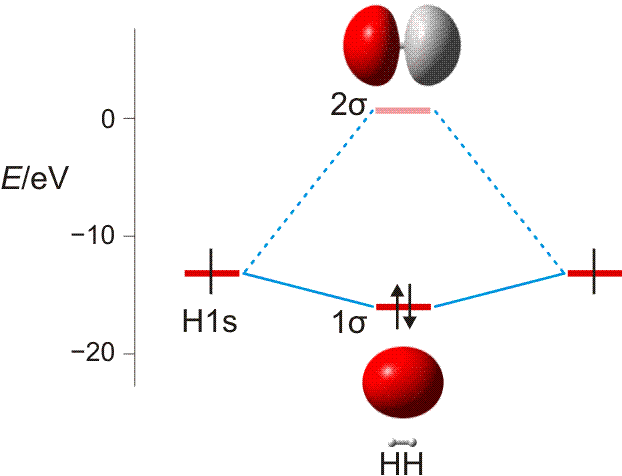
MO-Diagramm für H2. (Als Lage des antibindenden Orbitals ist die Energie des niedrigsten unbesetzten MOs des stabilen 1σ2 2σ0-Grundzustandes eingezeichnet.)
Technische Anmerkung: H2-Energien mit hf/aug-cc-pv5z bei 73,37 pm Kernabstand.
In zwei räumlich getrennten H-Atomen liegt das jeweils eine Elektron im kugelsymmetrischen 1s-Zustand vor. Nähern sich die beiden Atome nun einander, so gibt es zwei Möglichkeiten der Wechselwirkung: die Wellen verstärken einander (gleiches Vorzeichen der Wellenfunktion) oder sie löschen einander aus (verschiedenes Vorzeichen). Die erste Möglichkeit führt zu einer Lokalisierung der Elektronen zwischen den positiv geladenen Kernen und damit zur Bindung. Elektronen, die sich in diesem MO befinden, sind aufgrund ihrer Wechselwirkung mit zwei statt einem Kern gegenüber dem freien Atom stabilisiert, sie liegen auf der Energieachse unterhalb der Atomorbitalenergie – das MO ist bindend. Das Gegenteil trifft zu, wenn die beiden Wellen mit verschiedenem Vorzeichen miteinander kombiniert werden: es entsteht ein MO, das auf der Kernverbindungslinie eine Knotenebene aufweist. Ist dieses antibindende Orbital mit Elektronen besetzt, kommt es zur Lokalisierung von Elektronen jenseits der Proton–Proton-Achse, was einem unstabilen Zustand entspricht. Man beachte eine wichtige Regel: n Atomorbitale (hier 2) treten zu n Molekülorbitalen zusammen.
Der letzte Schritt bei der Konstruktion eines MO-Schemas ist das „Einfüllen“ der vorhandenen Elektronen. Analog dem Aufbauprinzip werden diese unter Beachtung von Pauli-Prinzip und Hundscher Regel auf möglichst stabile Zustände verteilt. Beim H2-Molekül wird dabei das bindende MO mit einem spingekoppelten Elektronenpaar gefüllt während das antibindende MO leer bleibt – es ist eine kovalente Bindung (Elektronenpaarbindung, Atombindung) entstanden. Das bindende MO ist dabei rotationssymmetrisch, es liegt eine σ-Bindung vor (vergleichen Sie die Symmetrieeigenschaften eines s-Orbitals). Die beiden Orbitale des Schemas werden mit 1σ und 2σ bezeichnet, üblich ist auch σ und σ* (sprich „sigma-Stern“), wobei der * das Orbital als antibindend markiert. Die Notation der Elektronenkonfiguration entspricht völlig dem Gebrauch bei Atomen; für den Grundzustand des H2-Moleküls 1σ2 2σ0.
Ein weiterer wichtiger Begriff ist die Bindungsordnung. Hierzu addiert man die Zahl der Elektronen in bindenden Molekülorbitalen (solche ohne Knotenebene senkrecht zur Kern-Kern-Achse), subtrahiert dann die Zahl der Elektronen in antibindenden MOs (solche mit Knotenebene senkrecht zur Kern-Kern-Achse) und dividiert durch zwei. Bei H2:
BO = (2 − 0)/2 = 1
Die beiden Wasserstoffatome werden durch eine Einfachbindung zusammengehalten.
Im folgenden Kapitel werden wir die Reaktion von Wasserstoff mit Chlor, Cl2, untersuchen. Die beiden Gase reagieren exotherm zu ebenfalls gasförmigem Chlorwasserstoff (Hydrogenchlorid), HCl, mit dessen Hilfe das Prinzip der nichtbindenden Wechselwirkung verdeutlicht werden soll.
Im Gegensatz zum Wasserstoffatom sind beim Chloratom aufgrund der Elektronenkonfiguration 1s2 2s2 2p6 3s2 3p5 auch p-Orbitale zu beachten. Gegenüber dem H2-Fall treten nun zwei neue Aspekte auf: (1) Welche Wechselwirkung tritt zwischen dem H(1s)- und den Cl(3p)-Orbitalen auf? (2) Wie ist die Wechselwirkung zwischen dem H(1s)- und dem Cl(3s)-Orbital, die auf der Energieachse recht weit auseinander liegen. Die folgende Abbildung zeigt die Antwort:
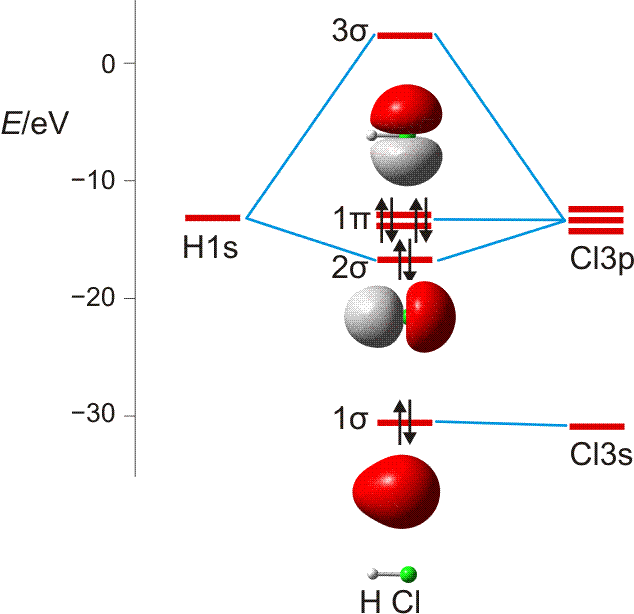
MO-Schema für HCl, Elektronen in Atomorbitalen weggelassen (technische Anmerkung: rmp2/6-31g(d,p), bei Cl über α- und β-Spins gemittelt, Ladung auf Cl nach Mulliken-Populationsanalyse: −0.17 e)
Von den drei 3p-Orbitalen des Chlors kombiniert nur eines mit dem H(1s)-Orbital zu einem bindenden (2σ) und einem antibindenden (3σ) MO. Es ist gerade dasjenige, das rotationssymmetrisch zur H-Cl-Bindungsachse liegt (die Wechselwirkung ist „symmetrieerlaubt“). Wird die H-Cl-Bindungsachse in einem kartesischen Koordinationsystem als z-Achse gewählt, so handelt es sich um das 3pz-Orbital.
Wird nun die Wechselwirkung zwischen dem H(1s)-Orbital und dem 3px- oder 3py-Orbital des Chlors betrachtet, so wird jeder konstruktiv interferierende Bereich durch einen gleich großen destruktiv interferierenden Bereich kompensiert. Die Orbitale sind orthogonal, die Wechselwirkung ist nichtbindend oder „symmetrieverboten“. Die beiden nichtbindenden p-Orbitale erscheinen im Schema energetisch unverändert (was nicht zwingend ist, vgl. weiter unten bei HF) und ohne Wechselwirkung mit dem H(1s)-Orbital.
Vom Ergebnis her ähnlich ist die H(1s)-Cl(3s)-Wechselwirkung im Diagramm behandelt. Das 1σ-Orbital erscheint bei fast derselben Energie wie das Cl(3s)-Orbital, außerdem scheint das H(1s)-Orbital nur wenig zur äußeren Gestalt von 1σ beizutragen – das ursprünglich kugelsymmetrische Cl(3s)-Orbital ist im 1σ-Orbital noch deutlich zu erkennen, allerdings ist es in Richtung auf das H-Atom „ausgebeult“. Das Orbital lässt sich in sehr grober Näherung als nichtbindend einstufen und dem Chloratom zuordnen. Es handelt sich dabei um eine quantitative Feststellung, denn prinzipiell führt die symmetrieerlaubte Wechselwirkung zu einer bindend-antibindend-Kombination und nicht zu einer streng nichtbindenden, symmetrieverbotenen Wechselwirkung – wir werden gleich darauf zurückkommen.
Zuerst aber das Ergebnis in der Übersicht: Je größer die Energiedifferenz zwischen zwei Orbitalen ist, desto kleiner ist die energetische Aufspaltung der MOs. Das Elektronenpaar ist räumlich an dem Atom lokalisiert, welches das Atomorbital mit fast gleicher Energie beisteuert. Bei der Berechnung der Bindungsordnung werden nichtbindende Orbitale nicht mitgezählt. Fünf Atomorbitale (1 von H, 4 von Cl) ergeben 1 bindendes, 1 ziemlich nichtbindendes, 2 streng nichtbindende und 1 antibindendes, insgesamt also 5 MOs, deren stabilere 4 jeweils 2 Elektronen enthalten. Es gilt:
BO = {2 (in 2σ) − 0 (in 3σ)}/2 = 1
Eine quantitative Aussage zur H(1s)-Cl(3s)-Wechselwirkung ist im MO-Formalismus wenig anschaulich. Im übernächsten Abschnitt wird daher zuerst am Beispiel des Cl2-Moleküls eine Methode vorgestellt, welche die MO-Theorie mit der nun zuerst vorgestellten Valenzbindungsmethode verbindet.
Lewis-Formeln erlauben die knappe Fornulierung von Elektronenpaarbindungen. Dargestellt werden die Elektronen der Valenzschale, ein Strich symbolisiert ein spingekoppeltes Elektronenpaar, ein Punkt ein ungepaartes Elektron. Die Elektronenkonfigurationen der Atome H (1s1), N (2s2 2p3 = 2s2 2px1 2py1 2pz1), O (2s2 2p4 = 2s2 2px2 2py1 2pz1), F (2s2 2p5 = 2s2 2px2 2py2 2pz1) und Cl (3s2 3p5 = 3s2 3px2 3py2 3pz1) im Grundzustand wird dargestellt als:
Bindungen entstehen durch Spinkopplung ungepaarter Elektronen zu Elektronenpaaren:
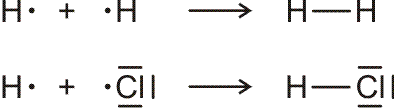
Lewis-Formeln sind oft hinreichend geeignet, das Ergebnis der Valenzbindungsmethode (engl. valence bond method, VB-Methode) darzustellen. Während bei der Molekülorbitalmethode sich über das ganze Molekül erstreckende Molekülorbitale (meist nach der LCAO-Methode) ermittelt werden, um anschließend die vorhandenen Elektronen nach dem Aufbau-Prinzip einzufüllen, sind Elektronenpaare bei der VB-Methode an einem Atom (einsame Elektronenpaare) oder zwischen zwei Atomen (bindende Elektronenpaare) lokalisiert. (Eine Delokalisierung über mehrere Atome kann oft durch „mesomere Grenzstrukturen“ beschrieben werden, auf die weiter unten eingegangen wird.)
Bei H2 und HCl führt das in den Orbitaldiagrammen zusammengefasste Verfahren, das im Wesentlichen der MO-Methode entspricht, aufgrund des nur einen Valenzorbitals an jedem H-Atom zu einem Ergebnis, das sehr dicht bei einer VB-Behandlung liegt. So ist es naheliegend, das 1σ-Orbital des H2-Moleküls als das bindenden Elektronenpaar der Lewis-Formel zu identifizieren. Beim HCl-Molekül zeigt das MO-Schema mit drei chlorständigen Orbitalen (1 π und 1σ) eine sehr ähnliche Situation wie die Lewis-Formel mit 3 einsamen Elektronenpaaren (engl. lone pairs). Das bindende Elektronenpaar der Lewis-Formel findet sich im MO-Schema im Wesentlichen als 2σ wieder.
Um den engeren Bezug von MO- und VB-Methode darzustellen, betrachten wir nun das Chlor-Molekül.
Am Chlormolekül, Cl2, soll gezeigt werden, dass es einen Zusammenhang zwischen MO- und VB-Behandlung gibt. Hierzu zuerst die VB-Methode. Ausgangspunkt sind zwei Chloratome und deren 3s23p5-Valenzkonfiguration. Nach der VB-Methode ist eine σ-Einfachbindung durch die Wechselwirkung der einfach besetzten pz-Orbitale zu erwarten:
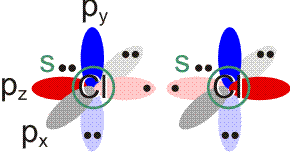
Als Lewisformel ausgedrückt:
Auch die MO-Methode geht von den Atomorbitalen aus und kombiniert diese zu bindenden und antibindenden MOs:
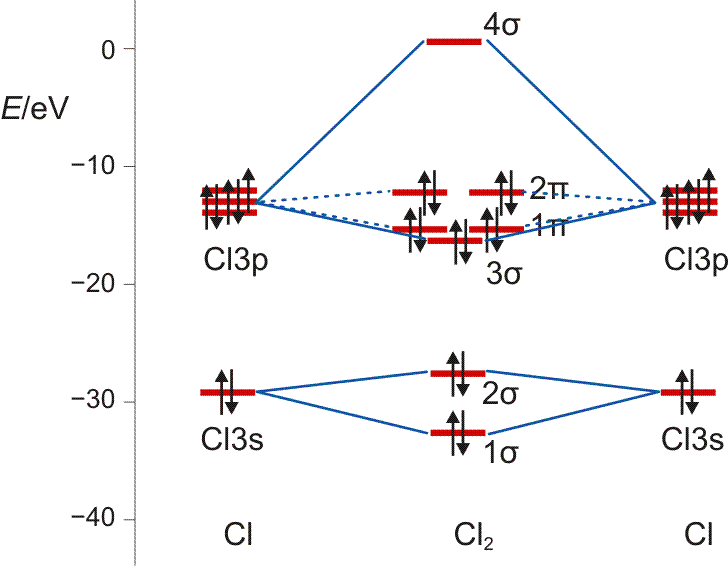
Wie bei H2 und HCl treten σ-Wechselwirkungen auf – sowohl bindende durch 3s-3s- und 3pz-3pz-Überlappung als auch eine antibindende 3s-3s-Wechselwirkung. Zusätzlich kommt durch seitliche Überlappung vom Typ 3px-3px und 3py-3py eine weitere Wechselwirkung hinzu, nämlich bindende und antibindende π-Molekülorbitale, die im Gegensatz zu den σ-Orbitalen nicht rotationssymmetrisch um die Bindungsachse sind, sondern in der Bindungsachse eine Knotenebene aufweisen.
Im folgenden Schema sind auf der linken Seite alle Molekülorbitale des Energiediagramms abgebildet. Zusätzlich ist das Ergebnis eines Rechenverfahrens gezeigt, mit dem immer dann eine VB-typische Betrachtung aus einer MO-Analyse abgeleitet werden kann, wenn sich die Valenzelektronen des betreffenden Moleküls in normale kovalente Bindungen und freie Elektronenpaare aufteilen lassen. Hierzu werden MOs (die zuvor durch Linearkombination aus AOs errechnet wurden) untereinander linearkombiniert. Für das Cl2-Molekül ist das Ergebnis besonders übersichtlich:
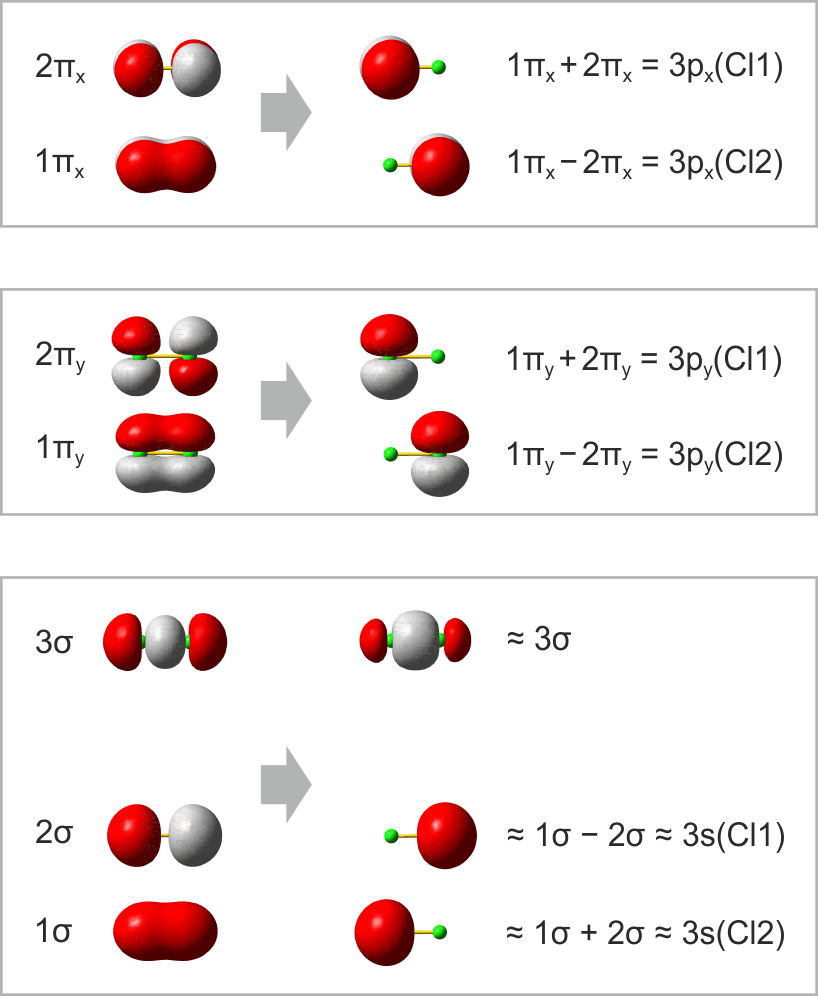
Das Ergebnis dieser Lokalisierung von MOs erschließt sich beim Vergleich mit der Lewis-Formel unmittelbar: ist in einem Molekül sowohl ein bindendes MO als auch das dazugehörige antibindende MO besetzt (linke Seite des Diagramms), so führt die Linearkombination des Paares zu jeweils einem freien Elektronenpaar an jedem Atom (rechte Diagrammseite). Da diese Bedingung für alle Orbitale außer dem 3σ-MO zutrifft, bleibt dieses als einziges beiden Chlor-Atomen zugeordnet. In der Lewis-Formel entspräche es dem bindenden Elektronenpaar, während die übrigen sechs Elektronenpaare mit den freien Elektronenpaaren der Lewisformel gleichgesetzt werden können.
Ein besonders nützliches Ergebnis des Verfahrens besteht in einer quantitativen Aussage, in welchem Umfang die Bindung – die vor allem durch die 3pz-3pz-Wechselwirkung entsteht – Anteile des Typs 3s-3pz enthält. (Vollziehen Sie als Vorübung nach, dass das auf der rechten Seite mit ≈3σ bezeichnete Orbital aus dem 3σ-MO entsteht, wenn in geringem Umfang 1σ subtrahiert wird). Für Cl2 bestätigt das Ergebnis den Eindruck, dass die Bindung vor allem 3pz-3pz-Charakter hat, indem jedes 3s-Atomorbital zu weniger als 10 % zur Bindung beiträgt.
Für das HCl-Molekül ist der Anteil höher. Die im MO-Schema von HCl sichtbare „Beule“ im 1σ-Orbital entspricht einem Anteil der H(1s)-Cl(3s)-Wechselwirkung von ca. 15 %, die wir näherungsweise vernachlässigt hatten. Der gemeinsame Beitrag von s- und p-Orbitalen zu einer Bindung wird im VB-Modell unter dem Stichwort „Hybridisierung“ behandelt. Wir führen dieses Konzept am Beispiel des N2-Moleküls ein, da dort die s-p-Wechselwirkung deutlich stärker ist.
Stickstoff ist der reaktionsträge Hauptbestandteil der Luft. Wie Wasserstoff, Chlor und auch Sauerstoff besteht Stickstoff aus zweiatomigen Molekülen. Die Elektronenkonfiguration des N-Atoms ist 1s2 2s2 2p3. Bei einer VB-Behandlung würden die drei ungepaarten p-Elektronen eines jeden Stickstoffatoms zu Elektronenpaarbindungen spingekoppelt:
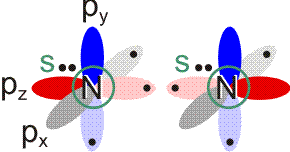
Durch Spinkopplung der beiden pz-Elektronen entsteht wie beim Cl2-Molekül eine σ-Bindung. Die beiden verbleibenden ungepaarten Elektronen eines jeden N-Atoms lassen sich zu zwei π-Bindungen koppeln. Insgesamt resultiert die Bindungsordnung 3. Das spingekoppelte Elektronenpaar im Grundzustand des N-Atoms (2s2) erscheint im Molekül als einsames Elektronenpaar bei jedem der beiden N-Atome. Mit Lewis-Formeln dargestellt:
Auch bei diesem nur zweiatomigen Teilchen liegt die MO-Behandlung noch nahe bei der VB-Betrachtung: Bei der Suche nach symmetrieerlaubten Wechselwirkungen führen die gleichen Überlegungen wie bei Cl2 zu zwei Gruppen von Atomorbitalen (die Bindungsachse sei auch hier die z-Achse): insgesamt vier 2s- und 2pz-Orbitale können in symmetrieerlaubter Weise kombiniert werden und ebenfalls vier 2px- und 2py-Orbitale liegen in nichtbindender Wechselwirkungen zu den Orbitalen der ersten Gruppe vor. Untereinander können die beiden 2px- und die beiden 2py-Orbitale zu zwei π-Wechselwirkungen kombiniert werden: zu bindenden MOs mt einer Knotenebene in der Molekülachse (1π) und antibindenden MOs mit einer Knotenebene in der Molekülachse und einer Knotenebene senkrecht zur Kernverbindungslinie (2π). In der Abbildung ist nur die π-Wechselwirkung in der Zeichenebene gezeigt (πy mit dem Koordinatensystem der VB-Betrachtung), nicht aber das dazu senkrecht stehende πx-Orbital.
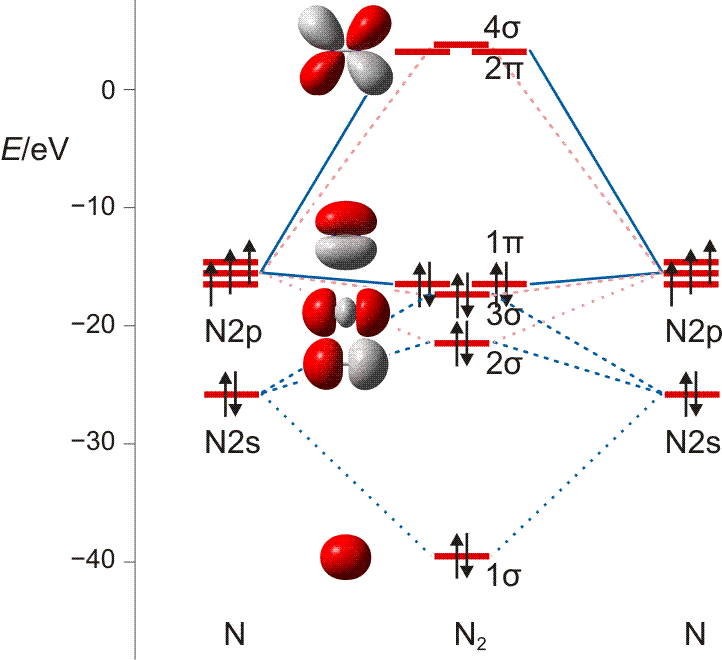
MO-Diagramm für N2 ( pdf). Es ist jeweils nur ein 1π und 2π-Orbital eingezeichnet. (Technische Anmerkung: das 2s-Orbital ist beim Mittelwert von α- und β-Spin eingezeichnet.)
Als Bindungsordnung ergibt sich durch Summieren über die aus 2 × 4 Atomorbitalen gebildeten 8 MOs:
BO = {2 (1σ) − 2 (2σ) + 2 (3σ) + 4 (1π) − 0 (2π) − 0 (4σ)}/2 = 3
Im Gegensatz zu Cl2 zeigen die σ-Wechselwirkungen nun eine merkliche Durchmischung von 2s- und 2p-Anteilen. Diese entdecken Sie auch dann, wenn Sie zuerst nur das MO-Schema analysieren.
Bei der VB-Methode wird die s-p-Wechselwirkung als Eigenschaft der Atomorbitale betrachtet. In der Praxis werden die MOs hierzu lokalisiert. Die beiden π-Bindungen bleiben hierbei als solche erhalten, da im Gegensatz zu Cl2 keine besetzten antibindenden π-Orbitale zur Linearkombination der MOs zur Verfügung stehen. Bei den σ-Orbitalen ist zu erwarten, dass das 1σ-2σ-Paar zu zwei freien Elektronenpaaren kombiniert werden kann. Die Rechnung ergibt das folgende Bild (links die MOs, rechts die lokalisierten Orbitale; unter beiden Orbitalgruppen ist zur Orientierung ein N2-Rumpf eingezeichnet):
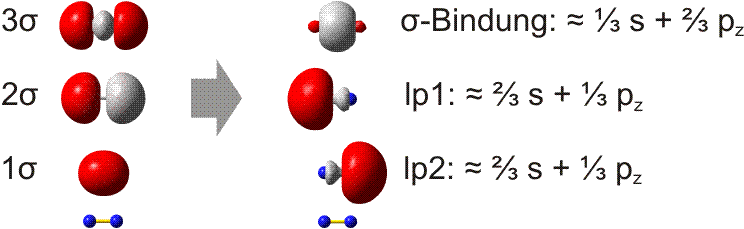
Weder das σ-Bindungsorbital noch die beiden freien Elektronenpaare (im Bild: lp1 und lp2) haben die Form, die für eine Wechselwirkung zwischen reinen s- oder p-Orbitalen zu erwarten ist. Die Rechnung ergibt dementsprechend die in der Abbildung angegebenen s- und p-Anteile. In der VB-Methode wird nun ein anschaulicher Formalismus eingeführt: die s-p-Mischung wird vor der Linearkombination zu Bindungen vorgenommen, indem s- und p-Atomorbitale zu Hybridorbitalen linearkombiniert werden. So entsteht eine Bindung mit zum Beispiel 35% s- und 65% p-Charakter durch Wechselwirkung zweier Hybridorbitale mit genau diesen s- und p-Anteilen:
Man beachte, dass die Summe der s- und p-Anteile der Gesamtzahl der Orbitale entsprechen muss: beim N2-Molekül addieren sich daher 1/3 s-Anteil der σ-Bindung und 2/3 s-Anteil des freien Elektronenpaars zu 1. Dasselbe gilt für das pz-Orbital. Das konkrete Ausmaß der s-p-Mischung ist eine charakteristische Variable in der Chemie der Hauptgruppenelemente. In Teil B der Vorlesung werden Trends im Periodensystem behandelt.
Die Beschreibung der chemischen Bindung durch den Lewis-Formalismus ist das einfachste Hilfsmittel, um ein Molekül darzustellen. Wenn sich lediglich die Frage nach Basisinformationen zu Molekülbau und -eigenschaften stellt (Ist das Molekül gewinkelt oder linear? Hat es ein Dipolmoment oder nicht?), reichen Lewis-Formeln oft aus.
Als Mindestanforderung an die Darstellbarkeit eines Moleküls durch eine Lewis-Formel sollte dabei verlangt werden, dass – notfalls durch die Formulierung der später im Detail behandelten „mesomeren Grenzstrukturen“ – (1) die Bindungsordnung und (2) der Spinzustand (Zahl der ungepaarten Elektronen) korrekt wiedergegeben wird. Von den besprochenen Molekülen trifft dies auf H2, HCl, Cl2 und N2 zu. Schon bei dem für das Leben wichtigsten Luftbestandteil, dem Sauerstoff, kommt die Lewis-Formulierung zu einer falschen Aussage.
O2 ist im Grundzustand paramagnetisch. Diese Eigenschaft zeigt, dass im O2-Molekül ungepaarte Elektronen vorhanden sind. Eine quantitative Behandlung zeigt, dass zwei ungepaarte Spins pro Molekül vorliegen. Dies ist nach der einfachen Formulierung einer Lewisformel nicht zu erwarten:
Allerdings zeigt sich schon bei einer näheren Betrachtung der zugrunde liegenden Atomorbitalwechselwirkungen, dass mit Schwierigkeiten gerechnet werden darf. Während sich nämlich bei N2 zwanglos zwei gleichwertige π-Bindungen aus vier gleichwertigen p-Orbitalen ergeben, zeigt dieselbe Ansicht für O2 ein Problem:
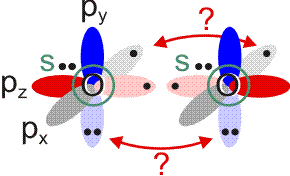
Obwohl geometrisch gleichwertig, sind die px- und py-Orbitale jetzt unterschiedlich besetzt – eines mit einem einzelnen Elektron, das andere mit einem Elektronenpaar.
Die MO-Rechnung ergibt ein Diagramm, das demjenigen des Stickstoffmoleküls sehr ähnlich ist. Wegen der um zwei größeren Valenzelektronenzahl ist nun jedoch der bei N2 leere 2π-Zustand mit zwei Elektronen besetzt und zwar wegen der Hundschen Regel mit jeweils 1 Elektron – O2 ist paramagnetisch. Die Beschreibung des Spinzustands ist als „Multiplizität“ gebräuchlich. Hierzu werden die ms-Werte zu einem Gesamtspin S addiert, anschließend wird die Multiplizität als 2S + 1 gebildet (für das Sauerstoffmolekül mit S = 2 × ½ = 1: 2 × 1 + 1 = 3). Teilchen mit einer Multiplizität von 1, 2, 3 sind im Singulett-, Dublett-, Triplett-Zustand. Die stabile Form von O2 ist also der Triplett-Sauerstoff.
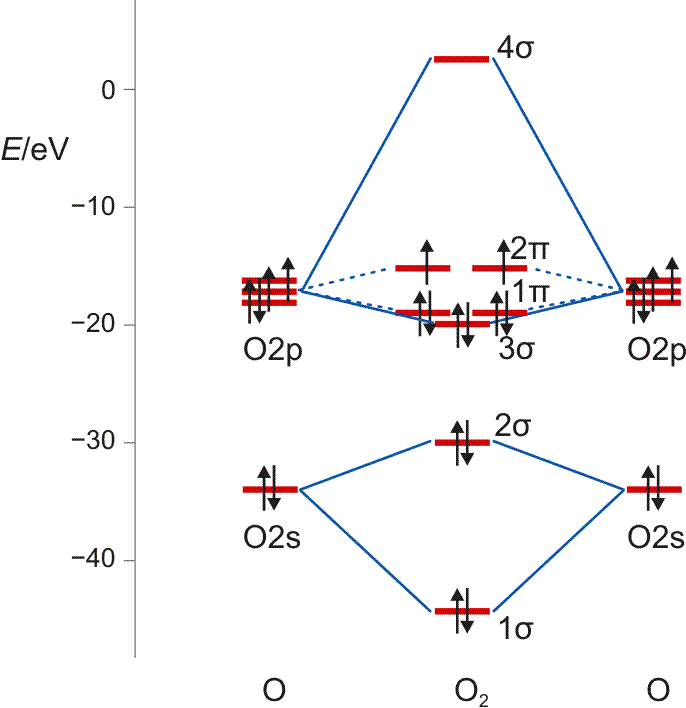
MO-Diagramm für O2.
Technische Anmerkung: O2-Energien und Atomabstand mit ump2/aug-cc-pvqz, 121,9 pm Atomabstand.
Während der Spinzustand durch eine Lewis-Formel nicht darstellbar ist, gibt es bei der Bindungsordnung Übereinstimmung. Aus der Abbildung ergibt sich auch bei der MO-Behandlung eine Doppelbindung:
BO = {2 (1σ) − 2 (2σ) + 2 (3σ) + 4 (1π) − 2 (2π)}/2 = 2
Sauerstoff, ein „Diradikal“, gehört zu den wenigen Molekülen, die stabil sind, ohne dass sich im Grundzustand für die Summe der (magnetischen) Spinquantenzahlen 0 ergibt, ohne also dass alle Elektronen spingepaart vorliegen. Zahlreiche chemische Reaktionen laufen nur ungehemmt ab (meist solche, bei denen keine Übergangsmetalle anwesend sind), wenn die Summe der ungepaarten Spins gleich bleibt. Entsteht bei einer solchen Reaktion Sauerstoff, so wird dieser nicht im Triplett-Grundzustand frei, sondern als unstabiler und äußerst reaktiver Singulett-Sauerstoff (den man mit der gezeigten Lewis-Formel beschreiben könnte).
Versuch 9.2: Singulettsauerstoff • Bei der Reaktion
H2O2 + Cl2 + 2 OH− → 1O2 + 2 Cl− + 2 H2O
wird Singulett-Sauerstoff gebildet. Bei der Rückkehr in den 3O2-Grundzustand wird rotes Licht der Wellenlängen 633 und 760 nm emittiert (190 = 2 × 95 und 158 kJ mol−1 entsprechend einer Emission zweier Singulett-Sauerstoff-Formen), hierzu Holleman-Wiberg: „… ist die Umsetzung von Hypochlorit mit Wasserstoffperoxid von einer Emission begleitet, die man mit dunkeladaptiertem Auge als roten Schimmer wahrnehmen kann.“
Das MO-Modell zeigte beim O2-Molekül seine Leistungsfähigkeit. Trotzdem kommt die Grundidee dieser Betrachtung – Orbitale über das gesamte Molekül zu delokalisieren – bei der Behandlung zweiatomiger Moleküle naturgemäß kaum zum Vorschein, da sich über nur zwei Atome nicht viel delokalisieren lässt. Viel klarer zeigen sich die Unterschiede zwischen MO- und VB-Methode, wenn mehratomige Moleküle betrachtet werden. Ein Musterbeispiel ist Methan, CH4.
Methan ist tetraedrisch aufgebaut, das heißt, die H-Atome bilden die Ecken eines Tetraeders, in dessen Schwerpunkt sich das Kohlenstoffatom befindet:
Schematisch (Erläuterung zur Schreibweise):
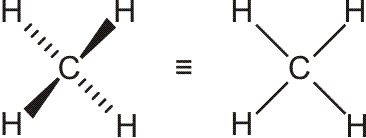
Bei der MO-Methode werden die Atomorbitale der vier H-Atome und des C-Atoms zu 5z-2e-Bindungen kombiniert – jedes Molekülorbital erstreckt sich also über alle Atome. Ausgehend von den Atomorbitalen des Kohlenstoffs wird hierzu jedes der vier Kohlenstoff-Valenzorbitale so mit einem Satz von jeweils vier H-ständigen Orbitalkombinationen linearkombiniert, dass sich vier bindende MOs ergeben. Bei den nicht besetzten antibindenden MOs sind die Vorzeichen der Wellenfunktionen vertauscht (entweder bei C oder beim H4-Teil):
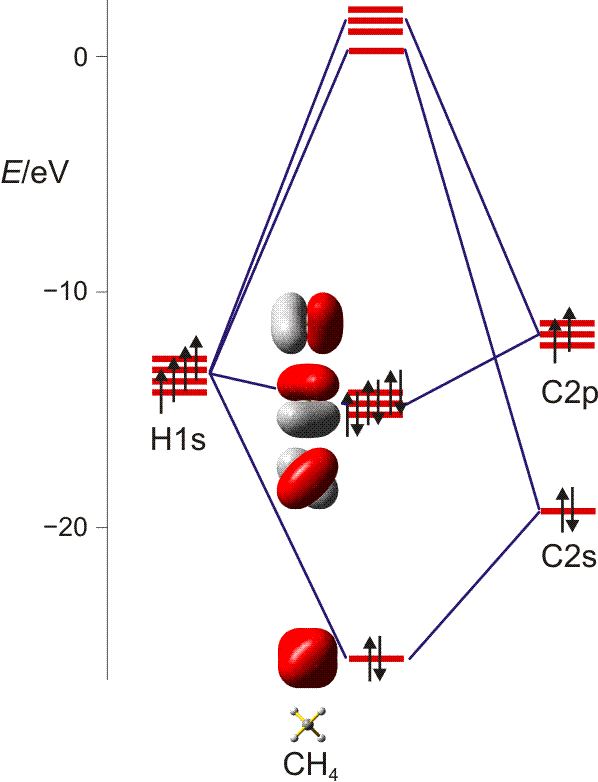
Schematisch:
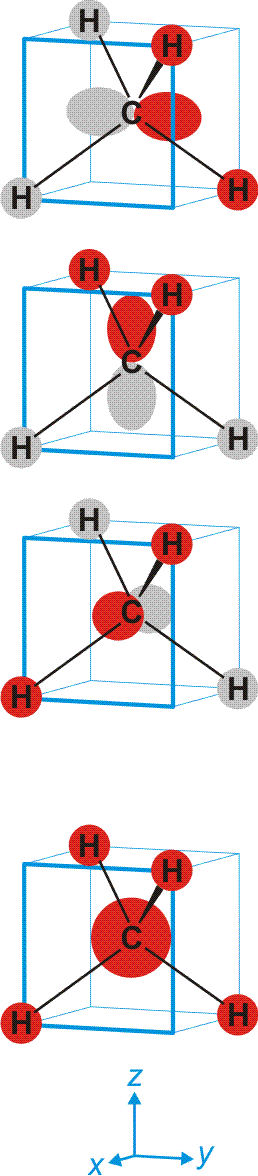
Man beachte, dass sich jeder einzelne der vier gleichwertigen C–H-Kontake aus vier Komponenten zusammensetzt. Da jedes bindende MO alle vier C–H-Kontakte einschließt, ist die Bindungsordnung für die einzelne C–H-Bindung 4 × ¼ = 1.
Wegen der hohen Symmetrie ist die Lokalisierung in 2z-2e-Bindungen übersichtlich: man überlagere zur Übung alle vier MOs des abgebildeten Schemas mit positivem Vorzeichen. Heraus kommt eine 2e-Bindung, zu der nur das 1s-Orbital des H-Atoms vorne rechts oben beiträgt sowie ein Hybridorbital am Kohlenstoffatom, das ¼ s- und ¾ p-Charakter hat. Dies gilt für alle Bindungen in diesem hochsymmetrischen Molekül. Wegen des dreifach höheren Gewichts der p-Orbitale an den vier gleichartigen Bindungen werden diese „sp3-Hybridorbitale“ genannt. (Es ist eine lehrreiche Übung, sich graphisch klar zu machen, dass zwei senkrecht aufeinander stehende p-Orbitale durch eine 25-%-ige s-Beimischung ihre Orthogonalität verlieren. Diese wird wiederhergestellt, wenn durch Vergrößerung des Winkels zwischen den Orbitalen deren gegenseitige Überlappung im verstärkten Bereich vermindert und im geschwächten Bereich vergrößert wird. Beim „Tetraederwinkel“ von 109.5° ist wieder Orthogonalität erreicht.)
Werden, wie in Lehrbüchern üblich, die VB-Orbitale nicht durch Lokalisierung aus MOs abgeleitet, beginnt das Aufstellen der Formel mit einem Problem. Ein Kohlenstoffatom im Grundzustand scheint mit seiner Valenzelektronenkonfiguration 2s2 2p2 nicht über vier einfach besetzte Orbitale zu verfügen. Im ersten Schritt wird daher ein energiereicherer 2s1 2p3-Zustand formuliert. Die benötigte Zahl ungepaarter Elektronen steht nun zur Verfügung. Durch Linearkombination wird nun die 2s1 2p3Konfiguration zu einer (sp3)4-Konfiguration hybridisiert. Die vier gleichwertigen Hybridorbitale weisen nun in die Ecken eines Tetraeders.
Alle vier Bindungen im Methan-Molekül sind äquivalent. Im Sinne des VB-Modells sind alle vier Elektronenpaare gleich hybridisiert. Eine grundlegend einfachere Betrachtungsweise als VB- und MO-Methode ergibt sich, wenn diese Eigenart des Methans auf alle denkbaren Moleküle übertragen wird – wenn wir also das Cl2-Molekül so verstehen, dass das bindende Elektronenpaar ebenso wie die freien Elektronenpaare sp3-Hybridorbitale darstellen. Da wir nur wenige Moleküle kennenlernen werden, bei denen diese Vereinfachung zulässig ist, werden wir diesem VSEPR-Modell (valence shell electron pair repulsion, Valenzelektronenpaarabstoßung) keine allzu große Aufmerksamkeit schenken (auf den schwerer wiegenden Nachteil, die wichtige Oktettregel nicht zu beachten, kommen wir noch zu sprechen). Beispiele für ein Moleküle, bei denen dieses Modell erfolgreich angewendet werden kann, sind NH3 und H2O. Das VSEPR-Modell wird daher im Kapitel „Polare Moleküle“ vorgestellt.
In der Vorlesung werden wir das Bindungsmodell verwenden, dass hinreichend – aber nicht unnötig – komplex ist, um die gerade interessierende Frage angemessen zu beantworten. Oft wird zur Beschreibung eines Moleküls die Lewis-Formel ausreichen. Die MO-Methode bietet sich gerade für Mehrzentrenbindungen an, hier wird jedoch auch auf mesomere Grenzformeln eingegangen, schon deswegen, da diese in den Lehrbüchern weit verbreitet sind.
Das Beipiel Methan zeigt besonders deutlich, in welchem Fall generell kaum auf die MO-Methode verzichtet werden kann, nämlich wenn es um Orbitalenergien geht. Wird Methan mit ähnlichen spektroskopischen Methoden untersucht wie sie oben für das H-Atom besprochen wurden, so zeigen sich im Grundzustand besetzte Orbitale bei zwei Orbitalenergien und nicht – wie es die VB-Betrachtung mit vier äquivalenten Hybridorbitalen nahelegt – nur eine einzige! Wann brauchen wir ein Modell, das Energien korrekt wiedergibt? Ein Beipiel ist die Besprechung von Halbleitern, die auf VB-Basis nicht sinnvoll beschreibbar sind. Ein anderes Beispiel ist die Beziehung zwischen der Farbe eines Stoffes und seiner Elektronenstruktur (warum ist Hämoglobin rot? Was lässt sich daraus schließen, wenn es bei der Wechselwirkung mit CO oder NO seine Farbe ändert?).
Für die meisten Elemente ist in den Lehrbüchern ein „Atomradius“ angegeben. Bei den nichtmetallischen Elementen handelt es sich dabei in der Regel um den kovalenten Einfachbindungsradius. Dieser ist definiert als die Hälfte des Atomabstandes in einer homonuklearen Einfachbindung. Beispiele: die Atomabstände in H2 und Cl2 betragen 74 und 198 pm. Die kovalenten Radien sind dann 37 und 99 pm. Mit Hilfe dieser Radien können Erwartungswerte für heteronukleare Bindungen errechnet werden. Für HCl ergibt sich so 136 pm (exp. 127 pm).
Zur Beschreibung polarer Atombindungen ist das Konzept der Elektronegativität hilfreich. Skalen wie die von Pauling oder Mulliken erlauben es, die Bindungspolarisation quantitativ zu erfassen. Polare kovalente Bindungen sind die Voraussetzung für Wasserstoffbrückenbindungen, die das Zustandsdiagramm des Wassers prägen.
| Mortimer: 8, 9,11 Binnewies: 5 Riedel: fehlt noch |
HCl bildet sich bei der Chlorknallgasreaktion in einer deutlich exothermen Reaktion. Bei dieser übersichtlichen Umsetzung, bei der aus 1 Molekül H2 und 1 Molekül Cl2 2 Moleküle HCl entstehen, ist die freiwerdende Energie gleich der Differenz der Bindungsdissoziationsenergie von HCl und dem Mittelwert der Dissoziationsenergien von Wasserstoff- und Chlormolekülen (siehe weiter unten). Warum ist die H–Cl-Bindung unerwartet stark? Dasselbe ist offensichtlich auch bei Wasser zu beobachten.
Auch die Eigenschaften von H2O und HCl, sowie auch die von dessen leichtem Analog HF, lassen sich durch eine einfache Atombindung allein nicht deuten. So neigt HCl außerordentlich stark dazu, auf andere Moleküle ein H+-Ion zu übertragen und dabei ein Cl−-Ion zu bilden (siehe unten im Kapitel „Säure-Base-Reaktionen“). Fluorwasserstoff, HF, ist darüber hinaus nicht, wie aufgrund der kleinen Molekülmasse zu erwarten wäre, bis hin zu tiefen Temperaturen ein Gas, sondern sein Siedepunkt liegt bei 19,5 °C. Dieses Verhalten wird plausibler, wenn für die HF- und HCl-Moleküle eine Polarisierung der Atombindung angenommen wird, wenn der Schwerpunkt des bindenden Elektronenpaars also eher zur Fluor- oder Chlor-Seite hin verschoben wäre. Eine übliche Formulierung für diesen Sachverhalt benutzt die Symbole δ+ und δ− über dem Atomsymbol, um eine Ladung andeuten, die ein Bruchteil der Elementarladung ist. Wie groß aber sind δ+ und δ−? Pauling stellte die erste Skala mit Werten für die Elektronegativität der Atome zusammen, bei der die Fähigkeit eines Atoms, das bindende Elektronenpaar einer kovalenten Bindung zu sich herüberzuziehen, in Zahlen gefasst war. Pauling war aufgefallen, dass eine hierdurch polare Bindung zwischen zwei Atomen eine höhere Bindungsdissoziationsenergie aufweist als erwartet (DHCl = 428 kJ mol−1, ½ DH2 + ½ DCl2 = 336 kJ mol−1). In der Formulierung
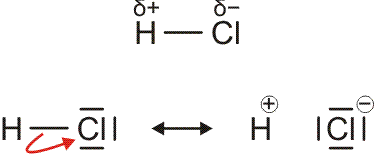
sollte sich eine Stabilisierung der Bindung durch die elektrostatische Wechselwirkung zwischen den Partialladungen ergeben – umso mehr, je größer der Betrag von δ ist. Die untere Formulierung beschreibt denselben Sachverhalt durch zwei mesomere Grenzformeln, die – mit unterschiedlichem Gewicht – zur beobachteten Elektronenverteilung beitragen.
Aus der Stabilisierung kovalenter Bindungen durch Dipolbildung leitete Pauling eine Elektronegativitätsskala ab, die ursprünglich auf den Wert 4.0 für das elektronegativste Element Fluor normiert war. Neben der Pauling-Skala sind weitere Skalen in Gebrauch, zum Beispiel die auf der Ladungsdichte des Atomrumpfes beruhende Allred-Rochow-Skala. Beachten Sie die Trends im Periodensystem.
Elektronegatvität (χ) einiger Elemente nach Pauling (P) und Allred-Rochow (AR):
| χ(P) | χ(AR) | |
|---|---|---|
| H | 2,20 | 2,20 |
| Li | 0,98 | 0,97 |
| Be | 1,57 | 1,47 |
| B | 2,04 | 2,01 |
| C | 2,55 | 2,50 |
| N | 3,04 | 3,07 |
| O | 3,44 | 3,50 |
| F | 3,98 | 4,10 |
| Ne | 4,84 | |
| Na | 0,93 | 1,01 |
| Mg | 1,31 | 1,23 |
| Al | 1,61 | 1,47 |
| Si | 1,90 | 1,74 |
| P | 2,19 | 2,06 |
| S | 2,58 | 2,44 |
| Cl | 3,16 | 2,83 |
| Ar | 3,20 | |
| Br | 2,96 | 2,74 |
| I | 2,66 | 2,21 |
Um die Polarität einer Bindung abzuschätzen, wird die Differenz von χ der beiden verbundenen Atome betrachtet. Der Ladungsschwerpunkt ist in einer polaren Bindung zum elektronegativeren Element hin verschoben. Auf der Pauling-Skala entspricht eine Elektronegativitätsdifferenz von 2 einer etwa 50-%-igen Ladungstrennung, das heißt, in der oberen Formel
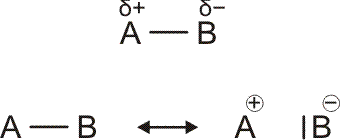
ist δ ca. 0.5; mit mesomeren Grenzformeln ausgedrückt würde ein Δχ von 2 einer Gleichgewichtung der beiden unteren Formeln, der kovalenten und der ionischen, entsprechen.
Da die Elektronegativität ein Maß für das Bestreben eines Atoms, einem Bindungspartner Elektronendichte zu entziehen, sein soll, erscheint unter den verbreiteten Elektronegativitätsskalen vor allem diejenige von Mulliken als unmittelbar einleuchtend. Er definiert EN-Werte als Mittelwert von 1. Ionisierungsenergie I1 und Elektronenaffinität EA, also als Mittelwert zweier Energiewerte, die das Zufügen und Wegnehmen eines Elektrons wiedergeben.
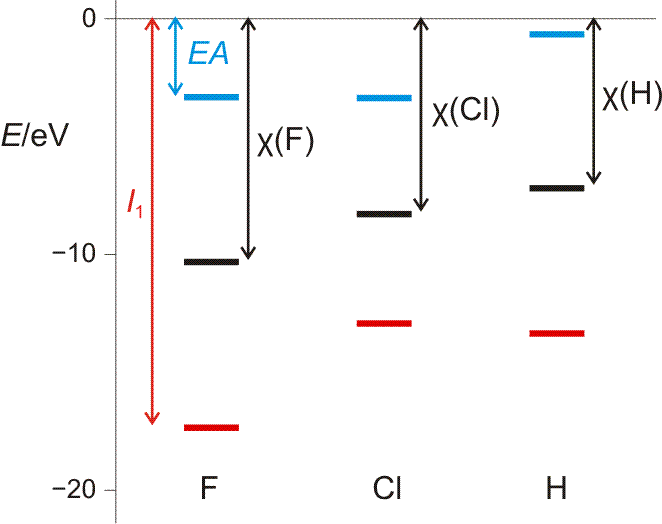
Die Mulliken-Elektronegativität, veranschaulicht mit den I1- und EA-Werten der Atome im Grundzustand (siehe Text).
Die Abbildung stellt den Bezug zu den oben verwendeten Orbitaldiagrammen her, zeigt aber nur das Prinzip des Verfahrens. Soll die Mulliken-Elektronegativität für die Analyse der Bindungssituation eines konkreten Moleküls verwendet werden, so zieht man die χMulliken-Werte für die einzelnen Atome in deren Valenzzustand (s/p-Anteile der Bindungen) heran, wodurch sich oft sehr unterschiedliche Werte für ein und dasselbe Element ergeben (das heißt für uns im Augenblick nur: überinterpretieren Sie nicht kleine Elektronegativitätsunterschiede!).
Das Konzept der polaren Atombindung beschreibt HF als Dipolmolekül (Dipolmoment = Ladung × Abstand der Ladungen). Während die Kräfte zwischen unpolaren Molekülen wie H2, N2 und O2 nur klein sind und diese Stoffe daher Gase mit außerordentlich niedrigem Siedepunkt sind, ziehen sich Dipolmoleküle elektrostatisch an, nachdem sie die günstigste Orientierung zueinander eingenommen haben. Mehr noch als HF ist Wasser das Dipolmolekül schlechthin. Wie HF entsteht auch Wasser in einer stark exothermen Reaktion aus gasförmigen Elementen. Der für ein so kleines Molekül erstaunlich hohe Siedepunkt von 100 °C zeigt an, dass beachtliche zwischenmolekulare (intermolekulare) Kräfte zwischen den H2O-Molekülen wirken müssen.
Das Wassermolekül zeigt sich bei den Methoden zur Strukturbestimmung als gewinkelt. Mit einer Elektronegativitätsdifferenz von ca. 1,3 ist jede der beiden H-O-Bindungen deutlich polar. Die beiden Bindungsdipolmomente addieren sich vektoriell zum Gesamtmoment.
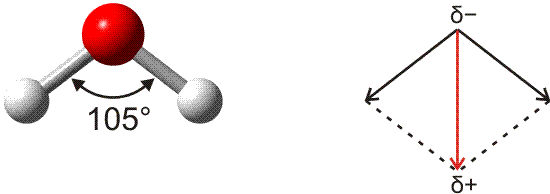
Versuch 13-4: Wasserdipole im elektrischen Feld
Der gewinkelte Aufbau des Wassermoleküls ist aus der Lewisformel unmittelbar ersichtlich, allerdings nicht mit dem Zahlenwert von 105°. Bei einer Bindung von zwei Wasserstoffatomen über die beiden halbbesetzten p-Orbitale eines Sauerstoffatoms sollte vielmehr mit einem 90°-Winkel gerechnet werden. Zu einer korrekteren – halbquantitativen – Aussage gelangt das VSEPR-Modell (valence shell electron pair repulsion, Valenzelektronenpaarabstoßung). In diesem einfachen Modell werden alle Valenzelektronenpaare als gleichwertig behandelt, es wird also nicht zwischen s- und p-Orbitalen unterschieden. Im Sinne des VB-Modells ausgedrückt: es wird von vollständiger Hybridisierung der Valenzorbitale ausgegangen, hier also von sp3-Hybridisierung.
Eine Strukturvorhersage wird nun anhand einiger einfacher Regeln getroffen. Die wichtigste: Die einander abstoßenden Elektronenpaare entfernen sich im Raum möglichst weit voneinander. Die vier Valenzelektronenpaare am Sauerstoffatom sollten damit in die Ecken eines Tetraeders weisen. Mit dieser Struktur ergibt sich für den H-O-H-Winkel zunächst ein Wert von 109,5°. Das Strukturmodell wird durch eine zweite Regel verfeinert: Einsame Elektronenpaare benötigen mehr Raum als bindende Elektronenpaare. Damit wird als Voraussage für den H-O-H-Winkel 109,5° − x erhalten, wodurch der gefundene 105°-Winkel nicht schlecht angenähert wird.
Die Eis-Ih-Struktur zeigt tetraedrische Umgebung um jedes Sauerstoffatom. Die Strukturanalyse zeigt fehlgeordnete Wasserstoffatome entlang der O-O-Verbindungslinien, die eine räumlich und/oder zeitlich gemittelte Situation widerspiegeln:
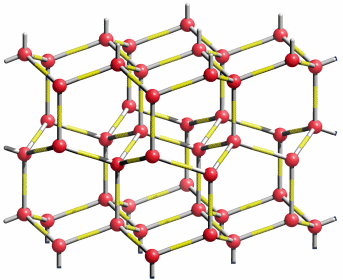
Die Struktur von Eis1h (gezeichnet in der Raumgruppe P 63/mmc). Die Wasserstoffatome sind „fehlgeordnet“, das heißt, dass die Wahrscheinlichkeit, sie auf der Bindung zum einem der vier nächsten O-Atome anzutreffen, jeweils ½ ist; man beachte 4 × ½ = 2 entsprechend der 2 H-Atome pro O-Atom im Wasser.
Eine reale Wasserstoffatomverteilung könnte so aussehen wie im folgenden Bild (hier dasselbe als bewegtes Bild):
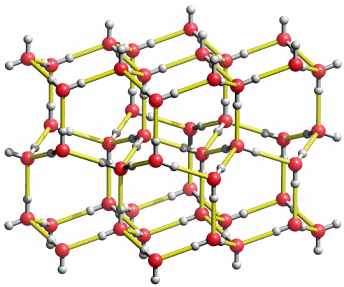
Die Struktur von Eis1h. So könnte eine „Momentaufnahme“ der wirklichen H-Atomverteilung in der mittleren Ebene der vorigen Abbildung aussehen. Durch Platzwechsel entlang der gelb eingezeichneten „Wasserstoffbrückenbindungen“ sind die H-Atome beweglich.
Die in die Eis-Ih-Struktur gelb eingezeichneten Wechselwirkungen sind Wasserstoffbrückenbindungen. Die tetraedrische Umgebung der Sauerstoffatome ist eine Folge dieser Bindungen:
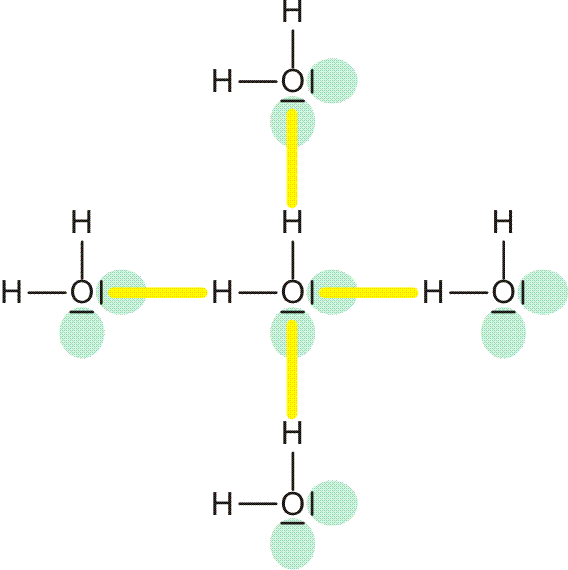
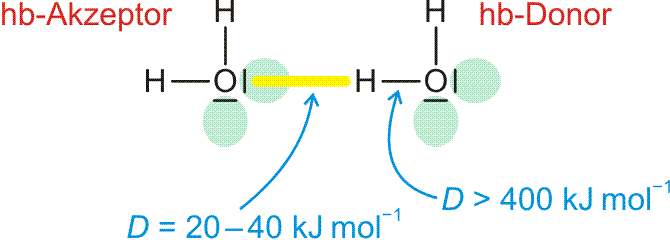
Wasserstoffbrückenbindungen sind durch folgende Merkmale charakterisiert: Das positiv polarisierte H-Atom eines Wasserstoffbrückenbindungsdonors (im folgenden Bild: „hb-Donor“) zeigt eine Wechselwirkung mit einem einsamen Elektronenpaar eines Wasserstoffbrückenbindungsacceptors („hb-Acceptor“). Die entstehende Wasserstoffbrückenbindung ist wie eine kovalente Bindung räumlich gerichtet, hat aber eine viel kleinere Bindungsdissoziationsenergie als diese. Vor allem hängt der Energiebetrag von der Umgebung ab. Ist die Bindung isoliert, ist die Dissoziationsenergie kleiner, ist die Bindung Teil eines Systems hintereinander oder auch cyclisch geschalteter O-H-Vektoren, ist die Energie größer, die Wasserstoffbrückenbindung ist dann Teil eines kooperativen Wasserstoffbrückenbindungssystems.
Durch die räumliche Ausrichtung der Bindungen ist in der Eisstruktur eine eher kleine Koordinationszahl realisiert, die Struktur ist im Vergleich zu dicht gepackten Salz- und Metallstrukturen „luftig“. Dies hat wichtige Konsequenzen für die Eigenschaften von Eis und flüssigem Wasser, die auch das Aussehen des Phasendiagramms bestimmen.
Versuch 13-1: Dichteanomalie
Versuch 13-3: Druckabhängigkeit des Schmelzpunktes von Eis

Die Dichteanomalie des Wassers im Druck-Temperatur-Diagramm. Der Tripelpunkt liegt bei 0,01 °C und 0,006 × 105 Pa (Normaldruck: 1,013 × 105 Pa), der kritische Punkt bei 374 °C und 220 × 105 Pa.
Beim Schmelzen von Eis entsteht eine Flüssigkeit, in der die Lücken der Kristallstruktur im Mittel verkleinert sind. Trotz dieser Kontraktion bleibt die Struktur des Eises jedoch ein gutes Modell für die Struktur des flüssigen Wassers. Vor allem das Prinzip, ein Wasserstoffbrückenbindungssystem aufzubauen, führt zur Formulierung eines Clustermodells des Wassers, in dem größere Molekülverbände („Cluster“) nach denselben Regeln organisiert sind wie Ausschnitte aus der Eisstruktur. Ein Beispiel für ein Bauelement, das kooperativ organisiert ist, ist der gezeigte viergliedrige „homodrome“ (gleichsinnig ausgerichtete ) Cyclus:
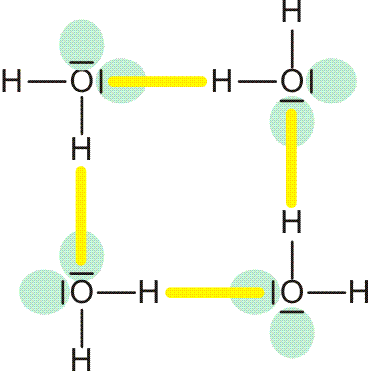
Vor allem, wenn der hb-Acceptor und der hb-Donor ohne H-Atom (demnächst: die konjugierte Base des hb-Donors) gleich sind, werden oft starke Wasserstoffbrückenbindungen gefunden, bei denen der Abstand zwischen Donor- und Acceptoratom kleiner als üblich ist. Bei besonders starken Bindungen ist das H-Atom symmetrisch angeordnet, so dass keine Unterscheidung zwischen Donor und Acceptor möglich ist. In diesem Fall lässt sich die Bindung durch mesomere Grenzstrukturen beschreiben; ein Beispiel ist das HF2−-Ion:

Man vergleiche eine normale und eine symmetrische, starke Wasserstoffbrückenbindung: Statt eines Donor-Acceptor-Abstands von 283 pm in Eis-Ih ist der F···F-Abstand im HF2− kleiner als 230 pm.
Eine Grenzsituation entsteht, wenn der hb-Acceptor eine höheres Bindungsvermögen für das Wasserstoffatom hat als der hb-Donor. Es kommt dann zum Übergang eines Protons auf den Acceptor, wobei das Reaktionsprodukt als wasserstoffbrücken-verbundenes Paar stabil sein kann:

Dieser Situation ist das Kapitel „Säure-Base-Reaktionen“ gewidmet.
Beim Wassermolekül ist die einfache Beschreibung mit Hilfe des VSEPR-Modells erfolgreich: wir nehmen vier gleichwertige Elektronenpaare an, die in der Sprache der VB-Theorie am Sauerstoffatom vier sp3-Hybridorbitale bedeuten. Die tetraedrische Umgebung des Wassermoleküls im Eis ergibt sich so recht zwanglos.
Wie sehen weitergehende Bindungstheorien das Wassermolekül? Wegen der Bedeutung des H2O-Moleküls benutzen wir dieses als Übunsobjekt, um noch einmal die wesentlichen Bindungsmodelle anzuwenden. Zuerst die MO-Theorie, bei der sich für das dreiatomige Wassermolekül neben einer nichtbindenden Wechselwirkung 2e-3z-Bindungen ergeben:
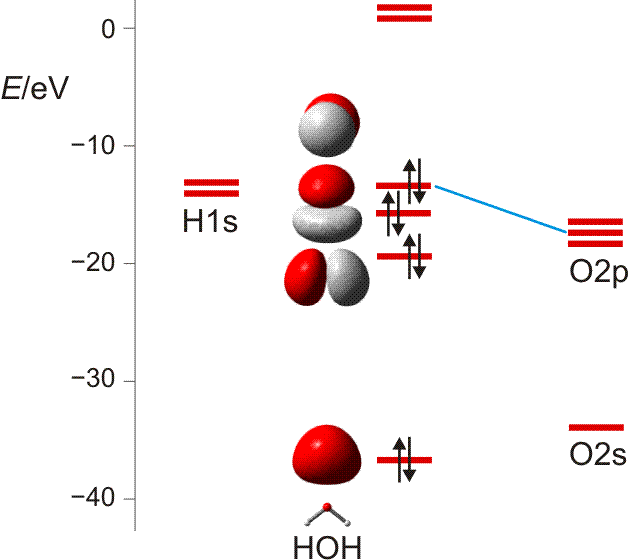
MO-Schema für H2O; Ladung auf O nach Mulliken-Populationsanalyse: −0.60 e (technische Anmerkung: rmp2/aug-cc-pvqz, bei O über α- und β-Spins gemittelt)
Zur Bindung zwischen O- und H-Atomen tragen alle besetzten MOs außer dem energiereichsten bei, das in nichtbindender Anordnung zu den H(1s)-Orbitalen steht. Die Wechselwirkung zwischen den beiden übrigen Sauerstoff-p- mit den H(1s)-Orbitalen führt zur Bindung, zu der auch das O(2s)-Orbital offensichtlich beiträgt (beachten Sie dessen Stabilisierung und die Abweichung von der Kugelgestalt, die es ohne H-Beteiligung hätte).
Etwas irritierend sind die MO-Energien. Wieso ist das nichtbindende Orbital unstabiler als im Atom? Kombinieren Sie zur Erklärung zwei bisher erarbeitete Ergebnisse: (1) Fluor-Valenzorbitale werden deutlich instabiler, wenn das Atom ein Elektron aufnimmt und zum Fluorid-Ion, dem F−-Ion, wird; (2) im polaren H2O-Molekül trägt das O-Atom ungefähr die Ladung −½e.
Wird die s-p-Mischung im Sinne des VB-Modells als Hybridisierung ausgedrückt, so ergeben sich bei der Rechnung O-H-Bindungen, zu denen das Sauerstoffatom zwei Orbitale mit ¼ s-Anteil beiträgt. Dieser Zahlenwert entspricht einer sp3-Hybridisierung, wenn mit gleichwertigen freien Elektronenpaaren formuliert wird (2 × ¼ s-Anteil in den Bindungen lassen ½ s-Anteil für beide freien e-Paare übrig, also ¼ für jedes e-Paar bei Gleichverteilung; eine alternative Sicht auf die freien e-Paare wird bei H2S in Teil B diskutiert). Es wird klar, dass immer dann, wenn die quantitative Behandlung zu Bindungen mit ca. 25% s-Charakter führt, das VSEPR-Modell gut dasteht, bei dem vollständige s-p-Mischung vorausgesetzt wird (Weiters hierzu in Teil B).
Der Grenzfall der polaren Atombindung bei hoher Elektronegativitätsdifferenz ist die Ionenbindung. Mit der Übertragung des bindenden Elektronenpaars auf das elektronegativere Element geht die räumliche Ausrichtung der Bindung verloren. Salzstrukturen zeigen daher andere Bauprinzipien als Strukturen, die durch kovalente Verknüpfung oder Wasserstoffverbrückung entstehen.
| Mortimer: 7, 20 Binnewies: 4, 7 Riedel: fehlt noch |
Die NaCl-Struktur ist eine prototypische Ionenstruktur. Als Bauprinzip fällt die dichte Packung der Kristallbausteine auf, bei der jede Ionensorte oktaederisch von Gegenionen umgeben ist:
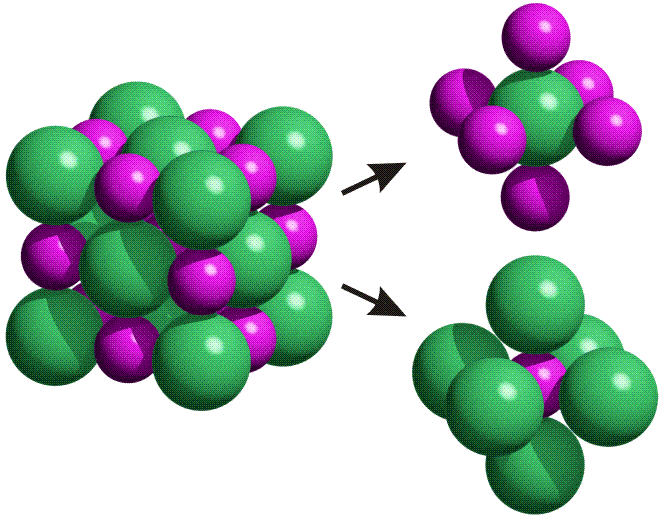
Die Bindung zwischen den Ionen ist weitgehend elektrostatisch. Die energetische Situation erschließt sich durch ein besonders aufschlussreiches Werkzeug, einem „Kreisprozess“. Vor allem die Beobachtung, dass bei der Bildung eines Salzes Ionen mit Edelgaskonfiguration entstehen, wird hierdurch in das richtige Licht gerückt.
Versuch 12-2: Synthese von Natriumchlorid aus den Elementen
Die Bildung eines Ionenkristalls aus den Elementen, die für das Beispiel NaCl mit der Energiebilanz
Na(s) + ½ Cl2(g) → NaCl(s) ΔHf0 = −411 kJ mol−1
abläuft, wird für die Formulierung eines Kreisprozesses in Teilschritte zerlegt. So ergeben sich für NaCl die folgenden Schritte mit den entsprechenden Energien:
(a) Die Bildung von einzelnen Na-Atomen aus festem Natrium, die Sublimationsenergie ΔHS0,
(b) die Bildung von einzelnen Cl-Atomen aus Cl2, die Bindungsdissoziationsenergie D,
(c) die Bildung eines Na+-Ions durch Ionisierung eines Na-Atoms, die 1. Ionisierungsenergie, I1,
(d) die Bildung eines Cl−-Ions durch Zufügen eines Elektrons zu einem Cl-Atom, die Elektronenaffinität EA,
(e) im letzten Schritt dann die Bildung des Ionenkristalls aus Na+- und Cl−-Ionen, die aus unendlicher Entfernung im Gasraum zum Kristall zusammentreten. Dieser Vorgang setzt die Gitterenergie Ug frei.
Die oben angegebene Standardbildungsenthalpie ΔHf0 ist die Summe aus diesen Einzelschritten:
ΔHf0 = ΔHS0(Na) + ½ D(Cl2) + I1(Na) + EA(Cl) + Ug
Für NaCl ergeben sich als Zahlenwerte (in kJ mol−1):
−411 = + 108 + 121 + 496 − 356 − 780
Die Energiebilanz zeigt, dass die Bildung der Edelgaskonfigurationen allein Energie benötigt: Der Vorgang
Na(g) + Cl(g) → Na+(g) + Cl−(g)
ist nämlich die Summe der Teilschritte:
Na(g) → Na+(g) + e−
und
Cl(g) + e− → Cl−(g)
Für den gesamten Vorgang ergibt sich:
ΔH0 = I1 + EA = +496 + (−356) = +140 kJ mol−1
Der Bildung von Na+- und Cl−-Ionen aus Na- und Cl-Atomen ist also endotherm. Eine wichtige Schlussfolgerung ist, dass beim Zuführen der Bindungsdissoziationsenergie zu NaCl die Ionenbindung genauso wie die kovalente Bindung unter Bildung von Atomen gespalten wird – die beiden wichtigen Grundtypen der chemischen Bindung verhalten sich also bei Zufuhr der Bindungsdissoziationsenergie gleich, beide werden homolytisch gespalten.
Der größte Einzelbetrag im Kreisprozess ist die Abgabe der Gitterenergie, also der Energie, die frei wird, wenn Ionen sich aus unendlicher Entfernung zu einem Ionengitter zusammenfinden. Zum stark exothermen Verlauf vieler Bildungsreaktionen von ionisch aufgebauten Stoffen aus den Elementen leistet die Gitterenergie meist den größten Beitrag.
Der erste Schritt beim Aufbau eines Ionenkristalls ist die Bildung eines Ionenpaares Na+Cl−. Der energetische Beitrag dieses ersten Schrittes zur Gitterenergie lässt sich berechnen. Bei der Annäherung von Na+- und Cl−-Ionen
• sinkt das zu r−1 proportionale Coulomb-Potential
| UC, Ionenpaar = | −z+ z− e2 |
| 4 π ε0 r |
allmählich (im Bild blau gestrichelt),
• steigt ein abstoßendes Potential schnell an (im Bild grün dargestellt; bei NaCl proportional zu ca. r−8), wenn der Abstand der Ionen einen Grenzwert unterschreitet, unterhalb dessen die Elektronenhüllen der Ionen in größerem Umfang einander durchdringen würden:
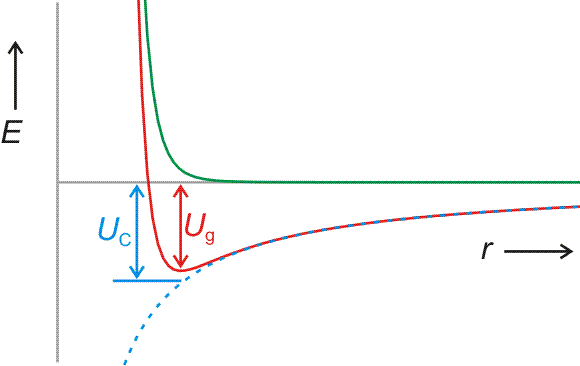
Der Zahlenwert der potentiellen Energie im Gleichgewichtsabstand (Ug im Bild) wird näherungsweise durch den Coulomb-Term allein bestimmt (UC im Bild). Für Na+Cl− (Kernabstand im Ionenpaar = 238 pm) ergibt eine solche Betrachtung −584 kJ mol−1. Verglichen mit der Gitterenergie von −780 kJ mol−1 zeigt sich, dass die Bildung des Ionenpaars Na+Cl− diesen Betrag zu einem großen Teil bewirkt. Die Berechnung erklärt das Verhalten von Salzen beim Verdampfen oder beim Auflösen in schlecht solvatisierenden Lösungsmitteln – hier liegen keine einzelnen Ionen vor, sondern Ionenpaare oder höhere Assoziate.
Um in ähnlicher Weise den Coulomb-Anteil UC an der Gitterenergie berechnen zu können, ist die Umgebung der Ionen zu betrachten. Für ein Na+-Ion im NaCl besteht diese Umgebung aus:
6 Cl− im Abstand d,
12 Na+ im Abstand √2 d,
8 Cl− im Abstand √3 d,
6 Na+ im Abstand √4 d = 2 d,
24 Cl− im Abstand √5 d, usw.
Die Coulomb-Energie der NaCl-Struktur ergibt sich als Summe der Einzelbeiträge, wobei die Häufigkeit der Abstände zu beachten ist; für r werden die entsprechenden Abstände als Vielfache von d eingesetzt, dem gefundenen Abstand zwischen den Ionen (im NaCl-Kristall 283 pm); z+ und z−, die Beträge der Ionenladungen (= 1 für NaCl) ist angegeben, da die Beziehung auch für andere Verbindungen mit diesem Strukturtyp gilt; anziehende Energiebeiträge werden mit negativem Vorzeichen eingesetzt, abstoßende positiv. Für 1 mol Salz gilt:
| UC = − | NA z+ z− e2 | (6 − 12/√2 + 8/√3 − 6/√4 + 24/√5 …) |
| 4 π ε0 r |
Der Klammerausdruck, der Grenzwert für unendlich viele Summanden, ist die Madelung-Konstante A, die nur vom Aufbau der Struktur abhängt. Für den NaCl-Strukturtyp ist der Zahlenwert 1,7476. Er gibt an, um welchen Faktor der Ionenkristall stabiler ist als ein gedachtes Ionenpaar, bei dem der Ionenabstand derselbe ist wie im Kristall. Die Gleichung für UC vereinfacht sich damit zu:
| UC = − | NA A z+ z− e2 |
| 4 π ε0 r |
Der vernachlässigte Abstoßungsterm trägt zu ca. 10 % zur Gitterenergie bei, um den die nur als UC abgeschätzten Werte vom Betrag her zu hoch ausfallen. Im Laufe der Zeit wurden verschiedene Näherungsverfahren beschrieben, um Ug präziser berechnen zu können. Verbreitet ist die Born-Landé-Formel:
| UC = − | NA A z+ z− e2 | (1 − 1/n) |
| 4 π ε0 r |
Hier wird ein Korrekturterm 1/n benutzt, der von der Elektronenkonfiguration der beteiligten Ionen abhängt. Er kann die folgenden Zahlenwerte annehmen:
| Konfiguration | Beispiel | n |
|---|---|---|
| [He] | H−, Li+ | 5 |
| [Ne] | O2−, F−, Na+, Mg2+ | 7 |
| [Ar], 3d10 | Cl−, K+, Cu+ | 9 |
| [Kr], 4d10 | Br−, Sr2+, Cd2+ | 10 |
| [Xe], 5d10 | I−, Cs+, Ba2+ | 12 |
Für NaCl ergibt sich im Rahmen der Born-Landé-Näherung mit NA = 6,022 ×1023 mol−1, A = 1,7476 für NaCl, e = 1,602 × 10−19 C, n = 8 als Mittelwert von 7 und 9, ε0 = 8,854 ×10−12 F m−1 = 8,854 ×10−12 C2 J−1 m−1, 2,83 × 10−10 m Ionenabstand in NaCl:
| UBorn = − | 6,022 ×1023 mol−1 × 1,7476 × (1,602 × 10−19 C)2 × (1 − 1/8) | = 751 kJ mol−1 |
| 4 π 8,854 ×10−12 C2 J−1 m−1 × 2,83 × 10−10 m |
Gitterenergien lassen sich nicht direkt messen, können als Zustandsgrößen aber indirekt bestimmt werden. Die im Kreisprozess verwendete Gleichung lässt sich zum Beispiel nach Ug auflösen; alle anderen Summanden können experimentell bestimmt werden. Man vergleiche den so erhaltenen Wert von −780 kJ mol−1 mit dem Wert von −751 kJ mol−1 nach der Born-Landé-Formel.
Werden verschiedene Verbindungen gleicher Struktur betrachtet, so ergibt sich aus der Betrachtung des Coulomb-Anteils eine Vergrößerung der Gitterenergie bei
• einer Erhöhung der Ladung der Ionen; man vergleiche Na+Cl− und Ba2+O2−:
NaCl (d = 283 pm), z+ = z− = 1: Ug = −780 kJ mol−1,
BaO (d = 276 pm), z+ = z− = 2: Ug = −3128 kJ mol−1,
Es folgt: Ug(BaO) ≈ 4 Ug(NaCl).
• einer Verkleinerung des Abstandes der Ionen; man vergleiche die Gitterenergie von BaO (d = 276 pm) mit dem Wert für MgO (d = 212 pm) von −3936 kJ mol−1.
Gitterenergien sind ein Maß für die Stärke der Bindung in einem Ionenkristall, sie sind daher zum Beispiel in der Reihe NaCl, BaO, MgO mit anderen physikalischen Eigenschaften wie dem Schmelzpunkt (800, 1925, 2642 °C) und der Härte (Ritzhärte nach Mohs: 2,5; 3,3; 6) verbunden.
Versuch 12-3: NaCl-Lösung leitet den Strom
Der kryoskopische Versuch hatte die Dissoziation von NaCl in Wasser gezeigt. Die Umgebung der Ionen im Kristall ist dabei Vorbild für die sehr ähnliche Umgebung in Lösung. Beim Auflösen des Salzes werden die Ionen von Wassermolekülen in der gleichen Weise umlagert wie sie im Kristall Gegenionen als Nachbarn hatten. So geht das NaCl6-Fragment des Kristalls in ein [Na(H2O)6]+-Ion in Lösung über. Das Natrium-Ion wird hydratisiert (allgemein: solvatisiert), es bildet sich ein Aquakomplex, hier das Hexaaquanatrium-Ion. An die Stelle der Chlorid-Gegenionen sind Wasserdipole getreten, die sich mit ihrem negativen Ende an die Kationen und mit der Gegenseite an die Anionen anlagern.
Die starke Analogie zwischen Ionenkristall und Lösung macht sich vor allem in der Energiebilanz bemerkbar. Die analog zur Gitterenergie definierte Hydratationsenthalpie (die bei der Hydratation von 1 mol Ionen freiwerdende Energie) hat annähernd denselben Betrag wie die Gitterenergie. Für NaCl (Gitterenergie −780 kJ mol−1) beträgt die Differenz zwischen Gitterenergie und Hydratationsenthalpie, die Lösungsenthalpie, nur 3,6 kJ mol−1.
Versuch 3-11: NH4NO3 löst sich endotherm
Versuch 12-8: CaCl2 löst sich exotherm, das Hexahydrat endotherm
Bei einem endotherm in Lösung gehenden Salz wie Natriumchlorid ist die Gitterenergie größer als die Solvatationsenthalpie. Hier stellt sich natürlich die Frage, warum sich NaCl überhaupt in Wasser auflöst?
Die bisher benutzte Näherung: „Exotherme Reaktionen laufen (spätestens nach Aktivierung) freiwillig ab, endotherme Reaktionen müssen durch laufende Energiezufuhr erzwungen werden“, gilt nur für Reaktionen mit starker Wärmetönung (vergleiche die Standardbildungsenthalpie von NaCl von −411 kJ mol−1 mit der Lösungsenthalpie von +3,6 kJ mol−1!). Maßgeblich für den freiwilligen Ablauf einer chemischen Reaktion, hier des Lösevorgangs, ist jedoch nicht die Reaktionsenthalpie. Vielmehr läuft eine chemische Reaktion (spätestens nach Aktivierung) freiwillig ab, wenn die Unordnung des Weltalls (als Summe der Unordnung des betrachteten Systems und der Unordnung der Umgebung) größer wird.
Zur quantitativen Beschreibung dient die Gibbs-Helmholtz-Beziehung:
ΔG = ΔH − T ΔS
ΔG ist die Änderung einer weiteren Zustandsgröße des betrachteten Systems, der freien Enthalpie G. ΔG ist mit der Änderung der Unordnung im Weltall verknüpft. Eine Vergrößerung der Gesamtentropie, der Bedingung für eine freiwillig ablaufende Reaktion, geht einher mit:
ΔG < 0
Die Gibbs-Helmholtz-Beziehung zerlegt die gesamte Entropieänderung in zwei Teile: der Entropieänderung in der Umgebung, die mit ΔH verknüpft ist (siehe oben) und der Entropieänderung im betrachteten System, ΔS.
NaCl löst sich in Wasser trotz des endothermen Reaktionsverlaufs auf, da aufgrund eines positiven T ΔS-Terms ΔG negativ wird. T ΔS ist positiv, wenn ΔS positiv ist, wenn also die Entropie des Systems größer wird. Für die Auflösung von NaCl ist dies einsichtig, da das geordnete Kristallgitter zerstört wird, und frei in der Lösung sich bewegende Ionen erzeugt werden.
ΔG, ΔH und T ΔS haben für einige Salze die folgenden Werte (in kJ mol−1):
| ΔH | T ΔS | ΔG | |
|---|---|---|---|
| NaCl | +3,6 | +12,8 | −9,2 |
| AgF | −20,3 | −5,8 | −14,5 |
| NH4Cl | +15,1 | +21,8 | −6,7 |
| MgCl2 | −155,0 | −29,0 | −126,0 |
Für Silberfluorid, AgF, und Magnesiumchlorid, MgCl2, ergeben sich negative T ΔS-Terme. Die Unordnung des Salz/Wasser-Systems nimmt beim Auflösen dieser Salze ab. Dies ist möglich, da beim Lösen zwar das geordnete Kristallgitter zerstört wird, auf der anderen Seite aber Wassermoleküle durch das Einfügen in eine Solvathülle geordnet werden. Erwartungsgemäß ist dieser Effekt bei MgCl2 mit seinem kleinen Mg2+-Kation hoher Ladungsdichte groß.
Ebenso wie sich die Reaktionsenthalpie ΔH0 als Summe von Standardbildungsenthalpien der einzelnen Reaktanden berechnen lässt, kann auch die freie Standardenthalpie ΔG0 einer Reaktion als Summe freier Standardbildungsenthalpien ΔGf0 berechnet werden. Die erhaltenen ΔG0-Werte gelten für Standardbedingungen bezüglich Druck und Temperatur, aber auch in Bezug auf die Konzentrationen der Reaktanden. Aus der Darstellung von ΔG als maximaler Nutzarbeit einer Reaktion (vergleiche Lehrbücher der Thermodynamik) lässt sich eine Beziehung zwischen ΔG und ΔG0 für andere Konzentrationen der Reaktanden herleiten. Für eine allgemeine Reaktion
a A + b B → x X + y Y
gilt im Falle verdünnter Lösungen:
| ΔG = ΔG0 + R T ln | [X]x [Y]y |
| [A]a [B]b |
Versuch 14-11: Iod in Wasser, KI-Lösung, Benzin, und Ethanol
Das aus völlig unpolaren Molekülen aufgebaute und daher hydrophobe Iod ist erwartungsgemäß in unpolaren Lösungsmitteln löslich, in Wasser dagegen praktisch unlöslich. Die Löslicheit in wässriger Kaliumiodid-Lösung ist daher völlig unerwartet. Den Schlüssel zum Verständnis dieses Phänomens gibt uns eine Strukturanalyse an dunkelbraunen Kristallen, die aus solchen Lösungen gewonnen werden konnten. Deren Formel ist KI3 · H2O; neben Kaliumionen und Wassermolekülen liegen Triiodid(1−)-Ionen, I3−, vor. Die Löslichkeit erklärt sich damit in der Umwandlung des hydrophoben I2-Moleküls in ein wasserlösliches Salz. Die I3−-Anionen sind linear aufgebaut:
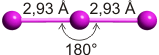
Die beiden gleich langen I-I-Atomabstände sind länger als im I2 (272 pm in festem Iod). Aufbau und Struktur des Anions sind sehr überraschend. Bei der Diskussion der chemischen Bindung traten bislang keine Spezies auf, bei denen ein Atom in seiner Valenzschale das Elektronenoktett überschreitet. Genau dies aber müsste angenommen werden, wenn mit den üblichen 2-Elektronen-2-Zentren-Bindungen formuliert würde:
Bei konventionellem Gebrauch der Valenzbindungsmethode würde man die Elektronenkonfiguration des mittleren Iodatoms mit sp3d angeben; es würde also ein d-Orbital hinzugenommen, um die zehn Elektronen am mittleren Iod unterzubringen. Nicht nur die Strukturanalyse, die eine geringere I-I-Bindungsordnung nahelegt, sondern auch die theoretische Behandlung der Bindung zeigt, dass die Beteiligung von d-Orbitalen nur untergeordnete Bedeutung hat (in einer Lewis-Formulierung: … die nur mesomere Grenzstrukturen mit geringem Gewicht hinzufügt). Wir berücksichtigen dies in der Vorlesung, indem wir in der Nichtmetallchemie stets die Oktettregel beachten.
Versuche, die Elektronenanordnung durch I3− in diesem Sinne realistischer zu deuten, sollten daher berücksichtigen: (1) das Oktett nicht zu überschreiten und (2) die aus den Bindungslängen hervorgehende Verminderung der Bindungsordnung zu erklären. Hier ein Versuch mit Lewis-Formeln, bei denen die kovalente Bindungsordnung ½ ist und das Oktett durch die Beteiligung eines ionischen Bindungsanteils erhalten bleibt:
Die beiden Grenzstrukturen beschreiben eine 4-Elektronen-3-Zentren-Bindung:
Eine solche Bindung wurde bereits behandelt, und zwar bei der starken Wasserstoffbrückenbindung im HF2−-Ion:
Die kovalente Bindungsordnung ergibt sich aus den Lewis-Formeln zu ½. Zu demselben Ergebnis führt eine Betrachtung der Molekülorbitale. Ein MO-Schema wird erhalten, indem jeweils 1 Atomorbital bei jedem Bindungspartner für das MO-Schema herangezogen wird (2p bei Fluor, 1s bei Wasserstoff). Kombination der drei Atomorbitale führt zu einem bindenden, einem nichtbindenden und einem antibindenden Molekülorbital; schematisch:
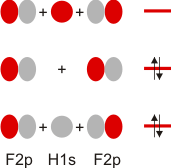
Das bindende und das nichtbindende MO sind mit jeweils zwei Elektronen besetzt. Die drei Zentren sind also durch ein Elektronenpaar verbunden, für den einzelnen F-H-Kontakt ergibt sich damit die Bindungsordnung ½. Die quantitative MO-Rechnung ergibt für die drei Orbitale:
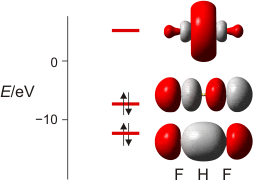
Die 4e-3z-Bindung im HF2−-Ion. Technische Anmerkung: Energien und Orbitale mit mp2/aug-cc-pvqz außer Gestalt des antibindenden Orbitals, diese mit hf/6-31g.
Im I3−-Ion ist auch das mittlere Orbital vom p-Typ. Schematisch:
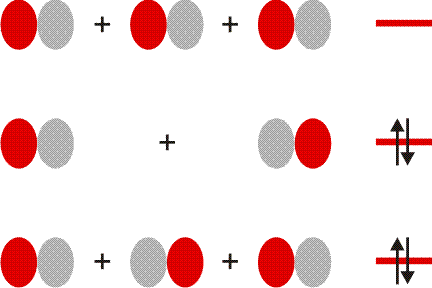
Die Bindungsordnung des einzelnen I-I-Kontakts ist wieder ½ – im Einklang mit der Lewis-Formulierung und den experimentell bestimmten Atomabständen.
Beim der Umsetzung gleicher molarer Mengen zweier Halogene bilden sich alle sechs denkbaren zweiatomigen Interhalogen-Verbindungen. So entsteht Chlorfluorid, ClF, als farbloses Gas gemäß
Cl2 + F2 → 2 ClF ΔH0 = −113 kJ mol−1
bei der exothermen Reaktion eines Cl2/F2-Gemischs bei Temperaturen unterhalb ca. 300 °C unter Kupferkatalyse.
Werden anstelle des 1:1-Gemischs 3 Teile Fluor und 1 Teil Chlor eingesetzt, so entsteht Chlortrifluorid, ebenfalls als farbloses Gas:
Cl2 + 3 F2 → 2 ClF3 ΔH0 = −330 kJ mol−1
Es können weitere Halogenfluoride hergestellt werden: neben BrF3 und IF3 die Halogen(V)-fluoride ClF5, BrF5 und IF5, sowie IF7, ferner ICl3.
Wie lässt sich die chemische Bindung in diesen Molekülen deuten? Bei ClF3 müsste die Valenzschale des Chloratoms Platz für 7 + 3 = 10 Elektronen aufbringen, wenn ausschließlich 2e-2z-Bindungen formuliert würden – wieder müssten d-Orbitale im Sinne einer sp3d-Hybridisierung beteiligt werden. Wie beim I3− zeigt die theoretische Behandlung jedoch eine nur geringe d-Orbital-Beteiligung an, so dass die Näherung „keine Beteiligung“ realistischer ist als „volle Beteiligung“. Solange wie zum Beispiel bei IF7 nicht die höchste Oxidationsstufe erreicht ist, wennn also noch mindestens 1 freies Elektronenpaar in der Valenzschale des Zentralatoms vorliegt, zeigen dieselben Rechnungen, dass das dann mit 2 Elektronen gefüllte s-Orbital als freies Elektronenpaar vorliegt und nur wenig zu den Bindungen beiträgt. Unter diesen beiden (etwas, aber nicht dramatisch) vereinfachenden Voraussetzungen – Bindungen nur mit p-Orbitalen des Zentralatoms, keine s-, keine d-Orbital-Beteiligung – kann die Struktur einer Interhalogenverbindung vorausgesagt werden.
Als Beispiel soll ClF3 eingehender behandelt werden. Die experimentelle Strukturbestimmung führt zu einer T-förmigen Gestalt des Moleküls:
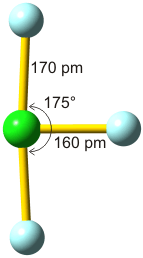
In der annähernd linearen F-Cl-F-Einheit sind die Fluoratome etwas zum dritten F-Atom hingeneigt. Die Cl-F-Abstände sind unterschiedlich: länger im annähernd linearen F-Cl-F-Fragment, kürzer bei der dritten Cl-F-Bindung.
Diese Struktur kann mit Hilfe des folgenden „Rezeptes“ vorausgesagt werden:
• (noch 'mal zur Sicherheit:) liegt das Zentralelement in der höchsten Oxidationsstufe vor? Wenn nein, so wie hier, weiter:
• Bilde 2e-2z-Bindungen. Notiere hierzu die Lewis-Formel des Zentralatoms und binde so viele Substituenten wie möglich bis das Oktett erreicht ist. Stelle die Orbitale der freien Elektronenpaare dar (das doppelt besetzte s-Orbital ist nur deswegen gezeichnet damit nichts fehlt, man kann es bis zur Lewis-Formel auch weglassen):
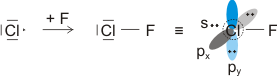
• bilde 4e-3z-Bindungen mit den restlichen Substituenten:
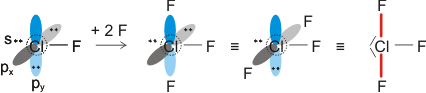
In eine Lewis-Formel übertragen, ergibt sich:
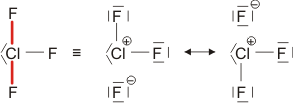
Die Lewisformeln verdeutlichen die Gültigkeit der Oktettregel sowie die Ungleichheit der Cl-F-Bindungen, die das Ergebnis der Strukturanalyse war: in der 4e-3z-Bindung ist die kovalente Bindungsordnung ½.
Die gezeigten mesomeren Grenzstrukturen werden nur dann großes Gewicht haben, wenn die Atome an den Enden der annähernd linearen X-Cl-X-Einheit hinreichend elektronegativ sind. Die Bedingung wird nicht mehr erfüllt, wenn die F-Atome zum Beispiel gegen H-Atome ausgetauscht werden. Es gibt daher HCl, nicht aber die zu ClF3, ClF5 und ClF7 analogen Moleküle H3Cl, H5Cl und H7Cl.
Sie können das beschriebene Verfahren nicht nur auf Interhalogene anwenden (siehe die nächsten Kapitel) und auch nicht nur auf neutrale Verbindungen, sondern auch auf Ionen.
Und jetzt zum unangenehmen Teil. Es gibt natürlich den Bedarf, den Aufbau eines Moleküls unkompliziert hinzuzeichnen; das heißt, zum Beipiel, ohne mesomere Grenzformeln. Es ist daher üblich, den Aufbau von ClF3 durch die Formel wiederzugeben:
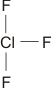
Dadurch wird natürlich unsere ganze Diskussion auf den Kopf gestellt. Wenn Sie eine solche Formel sehen, haben Sie zwei Möglichkeiten, diese aufzufassen: (1) sie denken sich: hier ist eine mesomere Grenzstruktur mit d-Orbital-Beteiligung aufgestellt; ich weiß, dass diese nur einen kleinen Anteil hat; sie wurde gewählt, weil sie am einfachsten hinzuzeichnen ist. (2) Sie begreifen diese Formel als topologische Formel, die nur den Aufbau einer Verbindung wiedergibt sowie eine Aussage darüber macht, welche Atome mit welchen irgendwie miteinander verbunden sind. Kürzer: ein Strich ist nicht immer eine 2e-2z-Bindung.
Beim Entwerfen der Lewis-Formel von Chlorat(V) begegnet uns ein bereits diskutiertes Problem: die Oktettaufweitung in vielen Büchern; auch hier formulieren wir im Einklang mit der Oktettregel gemäß
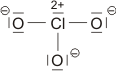
Eine technisch wichtige, aber doch brisante Verbindung ist Chlor(IV)-oxid (Chlordioxid). ClO2 gehört neben NO und NO2 zu den wenigen Radikalen, die als Substanz isolierbar sind:

Die mesomeren Grenzformeln haben annähernd das gleiche Gewicht, wie sich durch Rechnung zeigen lässt. Das ungepaarte Elektron besetzt das höchste besetzte Molekülorbital (HOMO), ein Cl-O-antibindendes Orbital vom π-Typ, mit annähernd gleichen Beiträgen der zugrunde liegenden Atomorbitale; im Bild liegt das Chloratom vorne, die beiden Sauerstoffatome weisen nach hinten:

XeF2, XeF4, XeF6 sowie das sehr unbeständige KrF2 entstehen bei der direkten Umsetzung der Elemente. Im Gegensatz zu Kryptondifluorid ist Xenondifluorid eine stabile Verbindung, die als farbloses kristallines Pulver kommerziell erhältlich ist.
Die im letzten Kapitel eingeführte 4e-3z-Bindung bestimmt die Strukturen und die Bindungsverhältnisse der Edelgasfluoride. Da bereits die Edelgasatome über ein Valenzelektronenoktett verfügen, gibt es keine 2e-2z-Bindungen in den Verbindungen der Edelgase. Das oben beschriebene Verfahren zur Vorhersage der Struktur beschränkt sich daher darauf, die entsprechende Zahl von Fluorpaaren an jeweils ein p-Orbital anzulagern. So ergibt die Vorhersage für Xenon(II)-fluorid eine lineare Struktur:
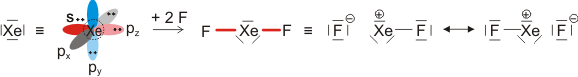
Für Xenon(IV)-fluorid wird auf demselben Weg quadratisch-planarer Aufbau vorhergesagt:
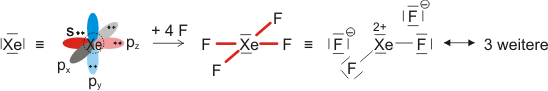
Das Experiment bestätigt beide Vorhersagen. Man beachte, dass sich wegen derselben Valenzelektronenanordnung dieselben Strukturen für ClF4− und für XeF4 ergeben.

Die Abnahme der s-Orbital-Beteiligung an den bindenden Elektronenpaaren von H2O zu H2S entspricht einem allgemeinen Trend im Periodensystem. Die s-Orbital-Beteiligung ist bei den leichten Elementen einer Gruppe größer als bei den schweren Homologen, wobei der größte Sprung zwischen der 2. und 3. Periode auftritt. Als Ursache wird oft die abnehmende Übereinstimmung der Bereiche größter Elektronenaufenthaltswahrscheinlichkeit genannt. Während bei 2s- und 2p-Orbitalen die maximale Aufenthaltswahrscheinlichkeit bei ungefähr gleichem Abstand vom Kern vorliegt, ist der s-Zustand bei größerer Hauptquantenzahl zunehmend kernnäher als die entsprechenden p-Orbitale.
Welche Werte ergeben sich konkret und welche Auswirkungen hat der zunehmend kleiner werdende s-Anteil bei den schweren Homologen auf deren Strukturchemie und deren Reaktivität?
Die Rechnungen zeigen hier eine deutliche Abhängigkeit der s-Orbitaltalbeteiligung vom jeweiligen Bindungspartner. Unter den einfachen und grundlegenden Verbindungsklassen werden besonders hohe s-Anteile in Bindungen von Nichtmetallatomen zu zwei Atomsorten gefunden: zu Wasserstoff- und zu Sauerstoffatomen (wirklich O-Atome, nicht OH-Gruppen, etc.!).
Die folgende Tabelle vergleicht die s-Anteile (in %) in Bindungen zwischen einem Nichtmetallatom und einem Wasserstoffatom in den einfachen Element-Wasserstoff-Verbindungen mit dem jeweiligen Element in dessen niedrigster Oxidationsstufe. (Techn. Anm.: mp2/cc-pvtz + nbo.)
| NH3 | 25 | H2O | 24 | HF | 21 | ||
| PH3 | 16 | H2S | 15 | HCl | 15 |
Werden anstelle der Element-Wasserstoff-Bindungen Element-Element-Bindungen betrachtet, so ergeben sich meist kleinere s-Beiträge. Die nächste Tabelle führt Moleküle mit jeweils einer Element-Element-Bindung auf, die außerdem meist noch Wasserstoffatome enthalten. Die nicht tabellierten s-Anteile der Element-Wasserstoff-Bindungen sind in etwa die gleichen wie bei den Verbindungen in der vorigen Tabelle. (Techn. Anm.: mp2/6-311+g(2d,p) + nbo)
| N2H4 | 26 | H2O2 | 12 | F2 | 6 | ||
| P2H4 | 12 | H2S2 | 10 | Cl2 | 7 |
Niedrige s-Anteile in Element-Element-Bindungen bedeuten, dass man sich diese ohne großen Fehler als Bindungen zwischen p-Orbitalen vorstellen kann. Da in diesem Bereich des Periodensystems die p-Orbitale die ungepaarten Elektronen enthalten – die Beteiligung von s-Orbitalen die Betrachtung also komplizierter macht –, stellen Moleküle wie Cl2 oder auch S8 (siehe unten) für die Bindungsbeschreibung kaum gestörte Normalfälle dar. Gedanklichen Aufwand verursacht ein scheinbar unkompliziertes Molekül wie Wasser!
Schwefel verbrennt in einer exothermen Reaktion zu Schwefeldioxid (ΔHf0 = −297 kJ mol−1):
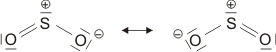
Man beachte die Formulierung, die im Einklang mit der Oktettregel erfolgt. Die Rechnung zeigt, dass die S-O-σ-Bindungen ca. 17 % s-Charakter aufweisen, das freie Elektronenpaar hat nahezu 70 % s-Charakter. Auch hier zeigt sich der typische Unterschied zwischen einem Element der zweiten und der dritten Periode: Ozon wird durch analoge mesomere Grenzformen beschrieben, die s-Anteile in den Bindungen und dem freien Elektronenpaar am mittleren O-Atom sind jedoch charakteristisch: 24 % in den Bindungen, 52 % beim freien Elektronenpaar.
SO2 ist ein Säureanhydrid. Mit Wasser wird schweflige Säure gebildet:
SO2 + H2O → H2SO3
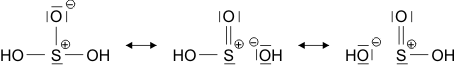
Bei der Formulierung der Lewis-Formeln wird auf ein Problem eingegangen, das durch die Absicht entsteht, die Oktettregel einzuhalten. Die linke mesomere Grenzformel zeigt das H2SO3-Molekül in der zum Beispiel bei Mortimer üblichen Weise. Hierbei haben alle Bindungen die kovalente Bindungsordnung 1, es wird also nicht zwischen der Bindung zur OH-Funktion und der zum O-Atom unterschieden. Hier ist die (zu vermeidende) hypervalente Formulierung mit 10 Elektronen hilfreicher, bei der durch eine Doppelbindung zum O-Atom hervorgehoben wird, dass diese Bindung die doppelte Bindungsordnung der S–OH-Bindungen hat. Eine realistischere Beschreibung des Moleküls unter Erhalt der Oktetts ist jedoch möglich, indem die beiden rechten mesomeren Grenzformeln hinzugenommen werden. Beachten Sie, dass diese Betrachtung auch auf weitere wichtige Moleküle zutrifft. Beispiele sind Schwefelsäure und Phosphorsäure.
Die Bildung von Schwefel-Schwefel-Bindungen führt zu Strukturelementen, die bei den Schwefelmodifikationen bereits sichtbar waren: Schwefelatomketten mit S-S-Abständen etwas oberhalb von 200 pm und Bindungswinkeln etwas oberhalb von 100°. Auffallend beim Tetrathionat vor allem wieder der fast rechte S-S-S-S-Torsionswinkel (abgebildet ist die Struktur des Anions in monoklinen Kristallen von K2S4O6):
Wie lässt sich dieses wiederkehrende Strukturelement verstehen? Hierzu zunächst ein Blick auf Schwefeldichlorid.
Schwefeldichlorid ist eine reaktive Verbindung, die technisch als Grundchemikalie hergestellt und in der Regel sofort weiterverarbeitet wird (SCl2 ist instabil gegen den Zerfall in Chlor und S2Cl2. SCl2 besteht aus gewinkelten Molekülen, die im Einklang mit der Oktettregel formuliert werden können:
Die Umgebung des Schwefelatoms im SCl2-Molekül ist derjenigen in Schwefelketten oder -ringen sehr ähnlich: der Abstand zu den Chlor-Nachbarn ist etwas größer als 200 pm (206 pm) und der Bindungswinkel ist etwas größer als 100° (104°). SCl2 gehört zu den Molekülen, für deren Formulierung sich nur eine einzige Lewis-Formel anbietet. Die Beschreibung durch lokalisierte Bindungen ist daher angemessen. Auch hier ist wenig Aufregendes zu finden; das folgende Bild zeigt eine der beiden gleichwertigen S-Cl-Bindungen:
Die dargestellte Bindung ist im Wesentlichen durch die Wechselwirkung eines S(3p)- und eines Cl(3p)-Orbitals entstanden. Der s-Anteil ist bei beiden Atomen klein; beim Schwefelatom wird ein Beitrag von 94 % p-Charakter nur durch 6 % s-Anteil modifiziert. Dementsprechend sind die beiden freien Elektronenpaare zu formulieren. Senkrecht auf der Ebene der drei Atome steht ein reines p-Orbital als eines der beiden freien Schwefel-Elektronenpaare. In der Ebene ist vom s-Orbital zweimal der 6-%-ige Beitrag zu den Bindungen abzuziehen, für das freie Elektronenpaar ergibt sich also 12 % p-Anteil und 88 % s-Charakter. Kurz: Vernachlässigen Sie im SCl2 jegliche Hybridisierung. SCl2 ist damit ein Molekül, dessen Bindungen sich sofort aus den beteiligten Atomen in deren Grundzustand ergeben.
Wie aber passt diese Aussage zum Bindungswinkel von 104°? Wir hatten bei Wasser und Schwefelwasserstoff gelernt, auf die Abstoßung zwischen Elektronenpaaren zu achten. Wird SCl2 hierauf untersucht, so fällt eine Gruppe von Orbitalen auf, deren Platzbedarf den erwarteten 90°-Bindungswinkel wirksam verhindert: die freien Elektronenpaare an den Chlor-Atomen und hier besonders die Elektronenpaare in p-Orbitalen. Die folgende Abbildung zeigt ein solches Orbital:
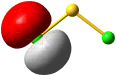
Es wird deutlich, dass sich das abgebildete Elektronenpaar und dessen Gegenüber am anderen Chloratom den Raum aufteilen müssen. Eine Verkleinerung des Cl-S-Cl-Winkels würde zu vermehrter van-der-Waals-Abstoßung führen, so dass der beobachtete 104°-Winkel die Balance darstellt zwischen dieser Abstoßung und dem Gewinn an Bindungsstärke bei optimaler Überlappung der Bindungsorbitale.
Auf diese einfache Weise erschließt sich auch die Strukturchemie der Schwefelketten und -ringe. In der folgenden Bilderserie ist dargestellt (von links): ein S8-Molekül mit Kronenstruktur, bei der vier Atome näher zum Betrachter hin liegen und vier darunter. Links daneben ist eine S-S-Bindung dargestellt, die völlig derjenigen im SCl2 entspricht (9 % s- und 90 % p-Anteil). Dementsprechend zerfallen die beiden freien Elektronenpaare an jedem Schwefelatom in ein Orbital, das im Wesentlichen s-Charakter aufweist und in ein reines p-Orbital, das senkrecht auf der Ebene steht, die neben diesem Schwefelatom dessen beiden nächsten Nachbarn enthält. In den beiden rechten Bilder sind zwei dieser Orbitale dargestellt. Es wird deutlich, dass die Abstoßung der freien p-Elektronenpaare minimiert wird, wenn diese im rechten Winkel zueinander stehen. Die Abstoßung zwischen freien p-Elektronenpaaren ergibt sich damit als die einfache Ursache für das häufige Auftreten von 90°-Torsionswinkeln.
Es wird erneut deutlich, welch komplizierter Sonderfall ein Wassermolekül darstellt, bei dem mehr Einflussgrößen als bei SCl2 und bei den Schwefelketten und -ringen in der realen Struktur ausbalanciert sind.
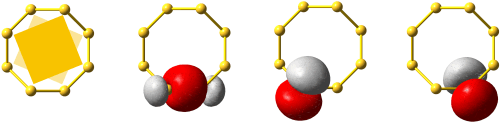
Die ungewöhnlichste Verbindung ist wohl das farblose Gas Schwefelhexafluorid, SF6. Während die Fluoride von Edelgasen und Halogenen – aber auch das näher verwandte SF4 – reaktive Fluorierungsreagenzien darstellen, ist SF6 unreaktiv: obwohl sich ein sehr deutlich negativer ΔG-Wert für die Spaltung der sechs S-F-Bindungen bei der Reaktion mit Wasser ergibt, findet selbst mit Wasserdampf von 500 °C keine Reaktion statt. SF6 wird wegen dieses Verhaltens technisch genutzt, zum Beispiel als unzersetzliches und elektrisch isolierendes Schutzgas in der Hochspannungstechnik. Die thermodynamischen Kennzahlen zeigen, dass SF6 keine besondere Stabilität aufweist. SF6 ist vielmehr inert, seine Unreaktivität ist auf ungewohnlich hohe Aktivierungsenergien für die Umsetzung mit Reaktionspartnern jeglicher Art zurückzuführen. Die mangelnde Reaktivität scheint mit der sterischen Abschirmung des Schwefelatoms durch sechs Fluoratome zusammenzuhängen:
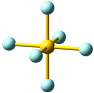
SF6 ist bedeutend genug, um an diesem Beispiel die Behandlung der Bindung in Molekülen fortzusetzen. Bisher war ein Fall nicht besprochen worden: wie werden Moleküle beschrieben, die bei der Annahme von 2e-2z-Bindungen das Valenzelektronenoktett überschreiten, bei denen das Zentralelement aber in der höchstmöglichen Oxidationsstufe vorliegt? Man erinnere sich an eine Vereinfachung, die bei Molekülen angewandt wurde, bei denen das Zentralelement noch mindestens 1 freies Elektronenpaar aufwies: diese Elektronen wurden dem s-Orbital zugewiesen und die Bindungen dann nur mit p-Orbitalen formuliert. Sind alle Valenzelektronen an der Verbindungsbildung beteiligt – was zum Beispiel der Fall ist, wenn die Oxidationsstufe der Zahl der Valenzelektronen entspricht – hat diese Vereinfachung natürlich keine Grundlage mehr.
In diesem Fall ist die Strukturvorhersage unaufwendig, dafür erfordert es mehr Mühe, die Bindungen im Einklang mit der Oktettregel zu beschreiben. Gehen Sie folgendermaßen vor:
• (zuerst wieder zur Sicherheit:) Liegt das Zentralelement in der höchsten Oxidationsstufe vor? Bei SF6 ist die Oxidationsstufe des Schwefels +VI, bei einem Element mit 6 Valenzelektronen also ja.
• Die Substituenten bilden in diesem Fall ein reguläres Polyeder um das Zentralatom und erreichen damit den größtmöglichen Abstand voneinander. Bei 4 Substituenten ist dies ein Tetraeder, bei 5 eine trigonale Bipyramide, bei 6 ein Oktaeder. Die Struktur von SF6 ist also oktaedrisch.
• Stelle den Beitrag der p-Orbitale des Zentralatoms fest: markiere hierzu lineare B-A-B-Einheiten, in denen 4e-3z-Bindungen auftreten und ordne jeder Bindung die kovalente Bindungsordnung ½ zu. Bei SF6 betrifft dies alle sechs Bindungen; jede erhält einen p-Beitrag zur Bindungsordnung von ½.
• Addiere den Beitrag des s-Orbitals des Zentralatoms: in einem regulären Polyeder überlappt das s-Orbital gleichwertig mit den Orbitalen aller Substituenten. Bei n Substituenten trägt diese Wechselwirkung zu 1/n zu jeder Bindung bei (Diese Wechselwirkung ist zum Beispiel im „Mortimer“ in Abb. 9.25 dargestellt, im „Riedel“ in Abb. 2.75a). Bei SF6 ist dieser Beitrag 1/6, die gesamte kovalente Bindungsordnung ist die Summe von s- und p-Anteil, also 2/3. Die Oktettregel ist damit erfüllt (6 × 2/3 × 2 Elektronen = 8 Elektronen).
Auf die bei SF6 angewandte Weise werden weitere Verbindungen mit scheinbarer Überschreitung des Elektronenoktetts behandelt. Eine für die weiteren Überlegungen wichtige Verbindung ist die Tellursäure H6TeO6 = Te(OH)6. Man beachte,dass hier gegenüber der Schwefelsäure eine formal wasserreichere Form mit erhöhter Koordinationszahl vorliegt.